概念問題 解答

高校数学　数学III

問題3の解答

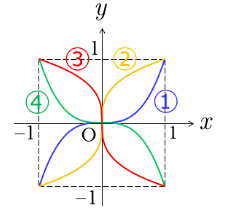
選択肢は

1．$y=x^3$， 2．$y=-x^3$， 3．$y=\sqrt[3]{x}$， 4．$y=-\sqrt[3]{x}$

である．

3のグラフは，$x<0$のとき$y>0$で，$x>0$のとき$y<0$となっている．

よって，$x>0$のとき$y>0$となる$y=x^3$と$y=\sqrt[3]{x}$は除外される．

$x=0$の近傍でグラフの傾きがマイナス無限大になっている．このような特徴があるのは残り$y=-x^3$と$y=-\sqrt[3]{x}$の内$y=-\sqrt[3]{x}$である．

以上より，答えは4となる．

■別解

1のグラフの関数は$y=x^3$であるとすぐに理解できる．

3のグラフは1のグラフを$y=x$に関して対称移動した後， $y$に関して対称移動したものである．

$y=x^3$ のグラフを $y=x$ に関して対称移動したグラフを表す関数 は

$x=y^3\to y=\sqrt[3]{x}$

となる．これを更に$y$ に関して対称移動した関数は

$y=\sqrt[3]{-x}\to y=-\sqrt[3]{x}$

となる

以上より，答えは4となる．