グラフを直線$y=x$に関して対称移動した関数

関数 ${\displaystyle y=f\left(x\right)}$  のグラフを 直線$y=x$に関して対称移動たグラフを表す関数は

${\displaystyle x=f\left(x\right)}$ 　･･････(1)

すなわち

${\displaystyle y=f^{-1}\left(x\right)}$ 　･･････(2)

となる．ただし，関数${\displaystyle f\left(x\right)}$ には，逆関数 ${\displaystyle f^{-1}\left(x\right)}$ が存在するものとする．

ポイント：直線$y=x$に関して対称移動した関数は元の関数の $x$と$y$を入れ換えたものになる．すなわち，元の関数の逆関数になる．

■式の導出

${\displaystyle y=f\left(x\right)}$ のグラフを直線$y=x$に関して対称移動したグラフを表す関数を求める．

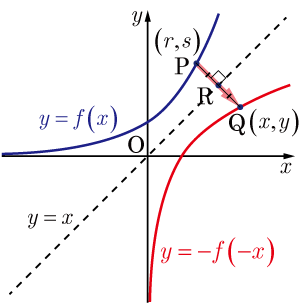
${\displaystyle y=f\left(x\right)}$ 上の点$\text{P}$を直線$y=x$に関して対称移動したものを点$\text{Q}$とし，点$\text{P}$，$\text{Q}$の座標をそれぞれ${\displaystyle \left(r,s\right)}$ ，$\left(x,y\right)$ とする．

まず，定直線に関して対称な点の条件より， $x$，$y$を$r$，$s$を用いて表すことにする．

線分$\text{PQ}$の中点を$\text{R}$とすると，点$\text{R}$の座標は

${\displaystyle \left(\frac{r+x}{2},\frac{s+y}{2}\right)}$

となり，点$\text{R}$が直線$y=x$上にあることより

${\displaystyle \frac{s+y}{2}=\frac{r+x}{2}}$　･･････(3)

が成り立つ．

また，線分$\text{PQ}$と直線$y=x$は直交することより

${\displaystyle \frac{y-s}{x-r}\cdot 1=-1}$　･･････(4)

ここで，${\displaystyle \frac{y-s}{x-r}}$は線分$\text{PQ}$の傾きである．

の関係がある．

(3)より

${\displaystyle x-y=s-r}$　･･････(5)

(4)より

${\displaystyle x+y=r+s}$　･･････(6)

(5)+(6)より

${\displaystyle 2x=2s}$ 　→　${\displaystyle x=s}$　･･････(7)

(6)-(5)より

${\displaystyle 2y=2r}$ 　→　${\displaystyle y=r}$　･･････(8)

(7)，(8)より

${\displaystyle {\displaystyle \left\{\begin{array}{l}x=s\\ y=r\end{array}\right.\to \left(x,y\right)=\left(s,r\right)}}$ 　　･･････(9)

備考：これは，直線$y=x$に関して対称移動すると，$x$ 座標と$y$座標が入れかわることを意味している．

の関係がある．これは点$\text{Q}$を点$\text{P}$の座標の値を用いて表しているが，逆に点$\text{P}$の座標を，点$\text{Q}$の座標の値$x$ ，$y$ を使って表すと

${\displaystyle \left\{\begin{array}{l}r=y\\ s=x\end{array}\right.\to \left(r,s\right)=\left(y,x\right)}$ 　･･････(10)

となる．点$\text{P}$は${\displaystyle y=f\left(x\right)}$ 上の点であるので

${\displaystyle s=f\left(r\right)}$ 　　･･････(11)

の関係がある．この(11)の$r$ と$s$に(10)の関係を代入すると

${\displaystyle x=f\left(y\right)}$　･･････(1)

となる．関数$f$の逆関数 $f^{-1}$ を用いて表すと

${\displaystyle y=f^{-1}\left(x\right)}$ 　･･････(2)

となる．(2)は$x$ と$y$の関係を表している．すなわち，この(2)が$y=f\left(x\right)$ のグラフを直線$y=x$に関して対称移動したグラフを表す関数である．

 

ホーム>>カテゴリー分類>>関数>>グラフを直線$y=x$ に関して対称移動した関数

最終更新日：2023年12月6日