概念問題 解答

線形代数　部分空間

問題1の解答

■ R 2 の 部分集合 W ′ が W 1 ， W 2 のように原点を通る直線の場合について部分空間になるかどうか検討する．

直線が y=ax とすると

W ′ = x y y=ax

となる．

W ′ が部分空間の条件を満たすかどうか検討する．

x 1 = x 1 y 1 ∈ W ′ ， x 2 = x 2 y 2 ∈ W ′ ， c∈R

とする．

x 1 + x 2 = x 1 + x 2 y 1 + y 2 = x 1 + x 2 a x 1 +a x 2 = x 1 + x 2 a x 1 + x 2

x 成分の a 倍が y 成分となっている．よって

x 1 + x 2 ∈ W ′ 　･･････(ii)

となる．

c x 1 =c x 1 y 1 =c x 1 a x 1 = c x 1 ca x 1 = c x 1 a c x 1

x 成分の a 倍が y となっている．よって

c x 1 ∈ W ′ 　･･････(ii)

となる.

(i),(ii)より， W ′ は部分空間の条件を満たしているので， W ′ は部分空間である．

上記の内容を図で示したのが下の図である．

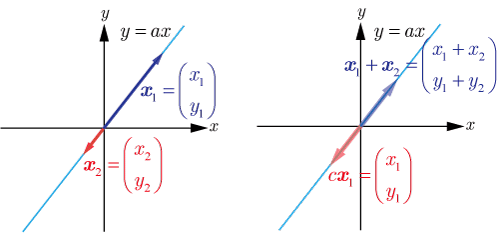
x 1 + x 2 の終点， c x 1 終点とも部分集合 W ′ の 直線上にあるので，部分空間の条件を満たしていることが分かるので， W ′ は部分空間であると判断できる．

■ R 2 の 部分集合 W ″ が W 3 のように原点を通らない直線の場合について部分空間になるかどうか検討する．

直線が y=ax+b とすると

W ″ = x y y=ax+b

となる．

W ″ が部分空間の条件を満たすかどうか検討する．

x 3 = x 3 y 3 ∈ W ″ ， x 4 = x 4 y 4 ∈ W ″ ， c∈R

とする．

x 3 + x 4 = x 3 + x 4 y 3 + y 4 = x 3 + x 4 a x 3 +b + a x 4 +b = x 3 + x 4 a x 3 + x 4 +2b

x 成分の a 倍プラス b が y 成分となっていない．よって

x 3 + x 4 ∉ W ″ 　･･････(iii)

となる．

c x 3 =c x 3 y 3 =c x 3 a x 3 +b = c x 3 c a x 3 +b = c x 3 a c x 3 +cb

x 成分の a 倍プラス b が y 成分となっていない．よって

c x 3 ∉ W ″ 　･･････(iv)

となる.

(iii),(iv)より， W ″ は部分空間の条件を満たしていないので， W ″ は部分空間である．

上記の内容を図で示したのが下の図である．

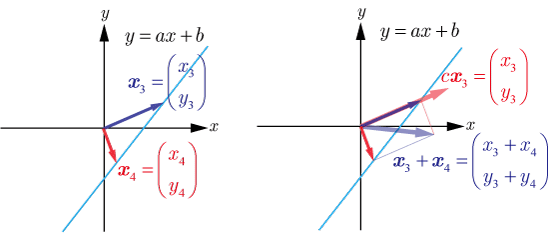
x 3 + x 4 の終点， c x 1 終点とも部分集合 W ″ の直線上にないので，部分空間であるための条件を満たしていないことが分かるので， W ″ は部分空間でないと判断できる．

■判断方法

原点を通る直線上の点の集合は部分空間になり，原点を通らない直線上の点の集合は部分空間にならない．