曲げモーメントの計算
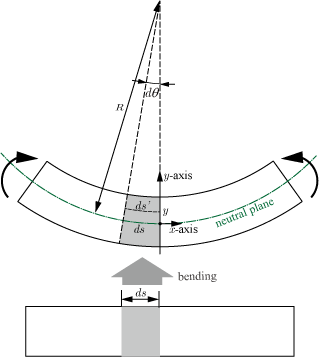 梁が図のように曲がったとき,灰色で示した梁の微少部分の右側断面に生じる曲げモーメント
梁が図のように曲がったとき,灰色で示した梁の微少部分の右側断面に生じる曲げモーメント
で表される.
■導出
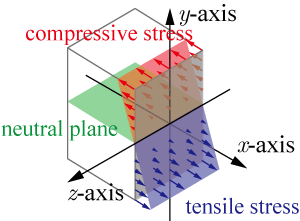
梁が曲がったときの応力分布は下の図のようになり,応力の値は
となる.曲げモーメントの値は
 ここで,
ここで,
となる.
最終更新日2018年2月4日
 梁が図のように曲がったとき,灰色で示した梁の微少部分の右側断面に生じる曲げモーメント
梁が図のように曲がったとき,灰色で示した梁の微少部分の右側断面に生じる曲げモーメント
で表される.
梁が曲がったときの応力分布は下の図のようになり,応力の値は
となる.曲げモーメントの値は
 ここで,
ここで,
となる.
最終更新日2018年2月4日