|
まず,
(1)より,
以上より, 1, となる。 理解をさらに深めるために求まった解を極形式に変えてみる(偏角
となり,複素数の絶対値が1で偏角が0°,120°,240°の120°間隔になっている特徴がある。
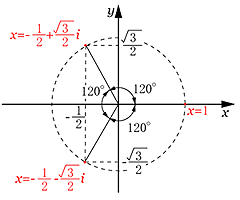
半径1の円上に この複素数の積の特徴を利用して,さらに
このような特徴を一般化したものがド・モアブルの定理であり,
[り] [ら行] [索引トップ] 
|
|
まず,
(1)より,
以上より, 1, となる。 理解をさらに深めるために求まった解を極形式に変えてみる(偏角
となり,複素数の絶対値が1で偏角が0°,120°,240°の120°間隔になっている特徴がある。

半径1の円上に この複素数の積の特徴を利用して,さらに
このような特徴を一般化したものがド・モアブルの定理であり,
[り] [ら行] [索引トップ] 
|
|
【表示調整】 現在の水平表示画素数 |