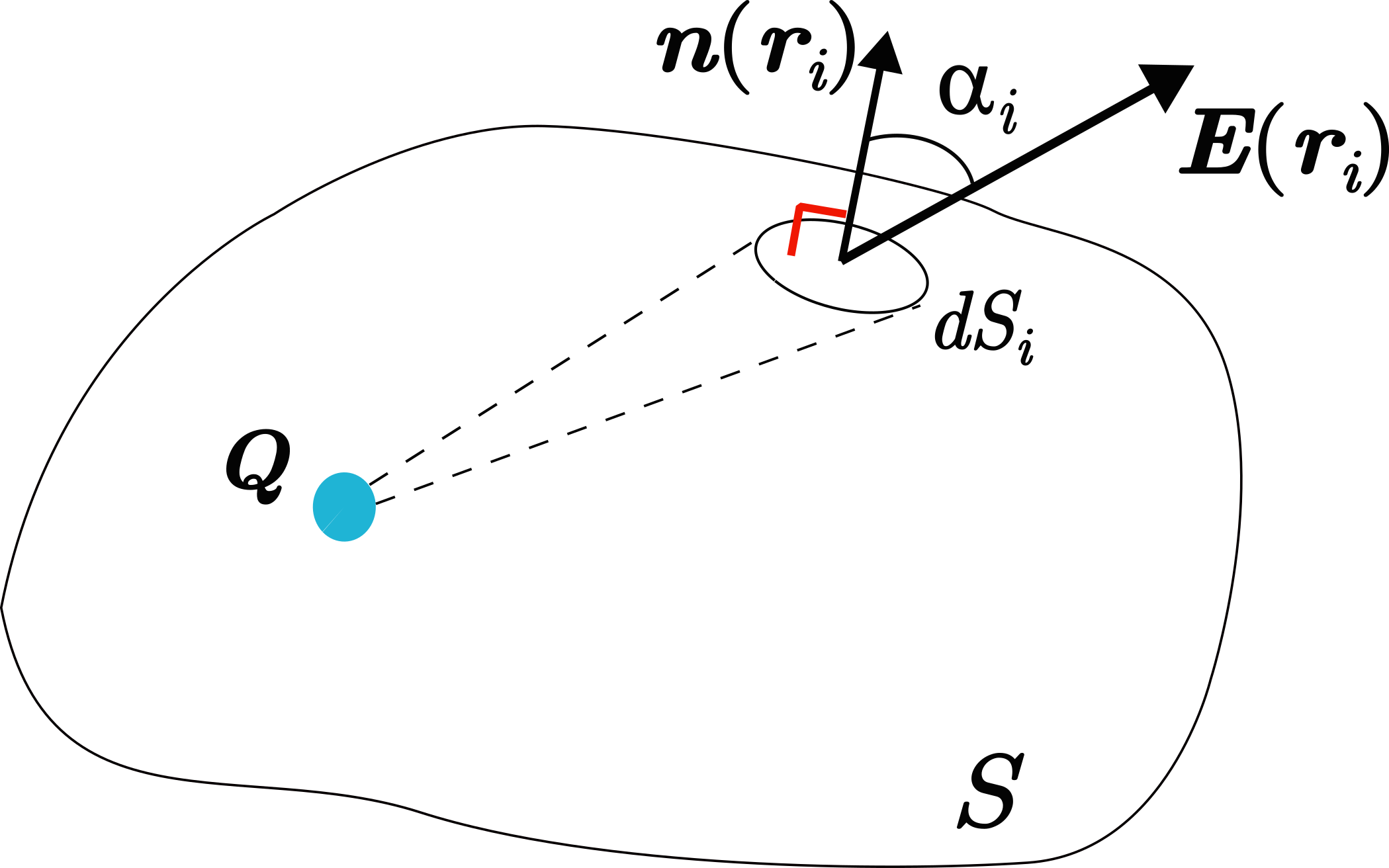
点電荷が閉曲面の内側にある場合のガウスの法則

[点電荷 ${\displaystyle Q}$ が閉曲面 ${\displaystyle S}$ の内側にある(電場と曲面が1回だけ交わる)場合]

曲面上の微小領域 ${\displaystyle d{S}_i}$ を考え，その位置ベクトルを ${\displaystyle r_i}$ ，単位法線ベクトルを ${\displaystyle n\left(r_i\right)}$ とする． ${\displaystyle d{S}_i}$ における電場ベクトル ${\displaystyle E\left(r_i\right)}$ と ${\displaystyle n\left(r_i\right)}$ のなす角を ${\displaystyle {\alpha }_i}$ とすると，2つのベクトルの内積は以下のようになる．

${\displaystyle E\left(r_i\right)\cdot n\left(r_i\right)=\left|E\left(r_i\right)\right|\left|n\left(r_i\right)\right|\cos {\alpha }_i}$

${\displaystyle \phantom{E\left(r_i\right)\cdot n\left(r_i\right)}=\left|E\left(r_i\right)\right|\cos {\alpha }_i=\frac{Q}{4\pi {\epsilon }_0}\frac{\cos {\alpha }_i}{r_i^2}}$

ここで， ${\displaystyle r_i}$ は点電荷から微小領域までの距離である．

次に，点電荷 ${\displaystyle Q}$ からみた ${\displaystyle d{S}_i}$ の立体角 ${\displaystyle d{\Omega }_i}$ について考える．

微小領域 ${\displaystyle d{S}_i}$ を点電荷を中心とする半径 ${\displaystyle r_i}$ の球面上に射影したときの面積を ${\displaystyle d{S}_i{}^{\prime }}$ とすると， ${\displaystyle d{S}_i{}^{\prime }=\cos {\alpha }_{i}d{S}_i}$ となる．また， ${\displaystyle d{S}_i{}^{\prime }:d{\Omega }_i=r_i^2:1}$ より ${\displaystyle d{S}_i{}^{\prime }=r_i^{2}d{\Omega }_i}$ である．これらを使うと，

${\displaystyle E\left(r_i\right)\cdot n\left(r_i\right)d{S}_i=\frac{Q}{4\pi {\epsilon }_0}\frac{\cos {\alpha }_i}{r_i^2}d{S}_i}$

${\displaystyle \phantom{E\left(r_i\right)\cdot n\left(r_i\right)d{S}_i}=\frac{Q}{4\pi {\epsilon }_0}\frac{d{S}_i{}^{\prime }}{r_i^2}=\frac{Q}{4\pi {\epsilon }_0}d{\Omega }_i}$

この式で${\displaystyle i}$ について和を取り，分割数が大きい極限で ${\displaystyle S}$ 上の面積分に置き換えると，

${\displaystyle {\displaystyle {\oint }_{S}E}\left(r\right)\cdot n\left(r\right)dS=\frac{Q}{4\pi {\epsilon }_0}{\displaystyle \oint d\Omega }=\frac{Q}{4\pi {\epsilon }_0}4\pi }$ ${\displaystyle =\frac{Q}{{\epsilon }_0}}$

が得られる．

よって，この場合も(1)式が成り立つことが確かめられた．

ホーム>>カテゴリー分類>>電磁気学>>ガウスの法則>>点電荷が閉曲面の内側にある場合のガウスの法則

学生スタッフ作成

2024年3月11日