ガウスの法則 (Gauss's law) 積分形

真空中に電荷があるとする．このとき，積分形のガウスの法則 (Gauss's law) は，

${\displaystyle {\displaystyle {\oint }_{S}E\cdot dS=}\frac{Q}{{\epsilon }_0}}$ ･･････(1)

の式で表される．ここで， ${\displaystyle S}$ は空間内に取った閉曲面， ${\displaystyle E}$ は ${\displaystyle S}$ 上の電場ベクトル， ${\displaystyle Q}$ は ${\displaystyle S}$ 内にある電荷の総量である．また， ${\displaystyle {\epsilon }_0}$ は真空の誘電率を表す．(1)式は， ${\displaystyle S}$ における電場ベクトルの面積分が， ${\displaystyle S}$ 内の電荷の総量を ${\displaystyle {\epsilon }_0}$ で割ったものに等しいことを示している．

以下では，まず単純な系として，半径 ${\displaystyle R}$ の球面の中心に点電荷 ${\displaystyle Q}$ がある場合を考え，(1)式が成り立つことを確認する．

[閉曲面 ${\displaystyle S}$ を半径 ${\displaystyle R}$ の球面とし，その中心に点電荷 ${\displaystyle Q}$ がある場合]

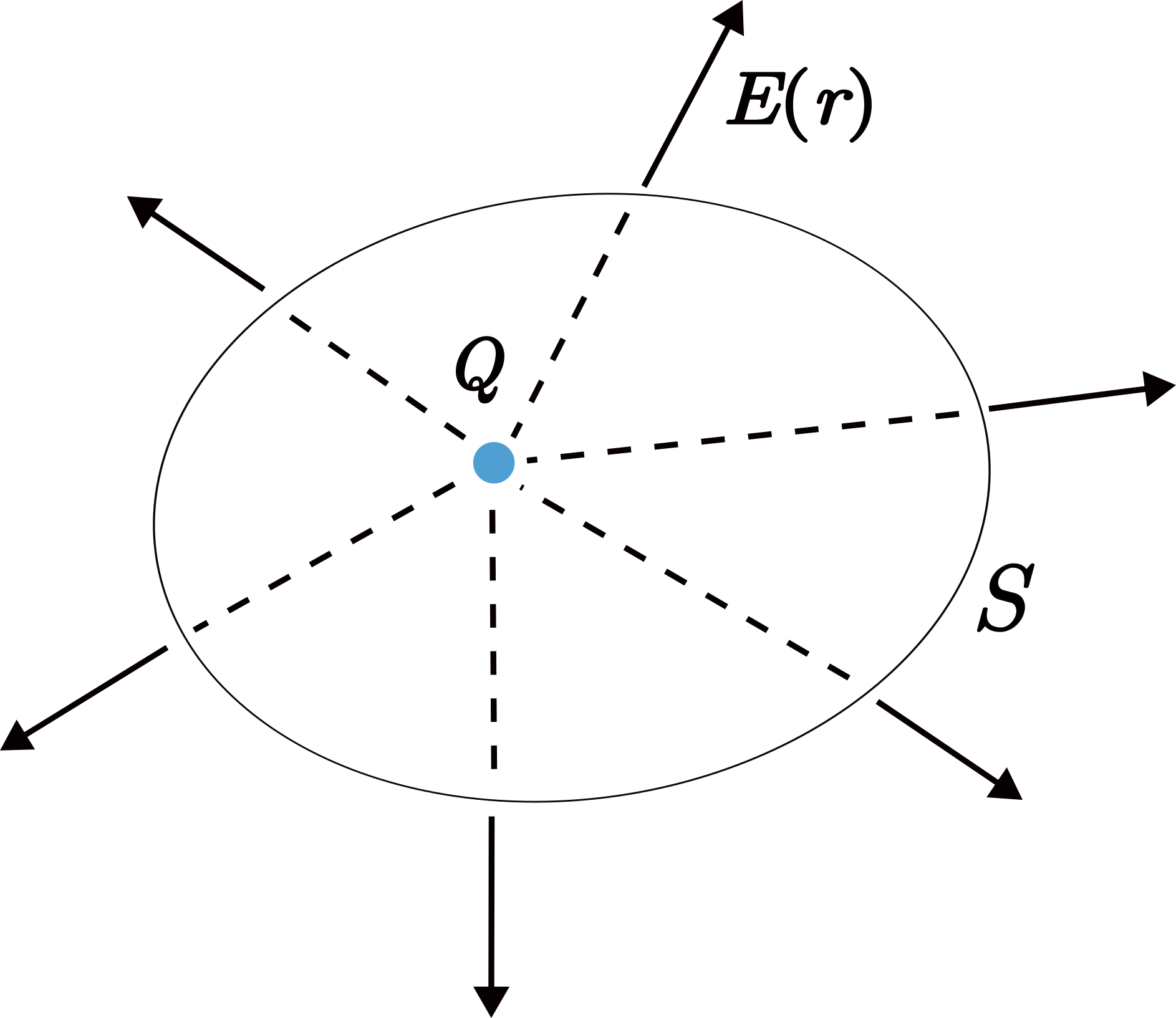
次に，任意の閉曲面や電荷について考える．ここでも単純な場合から考えることにし，1つの点電荷のみが閉曲面 ${\displaystyle S}$ の�@内側にある場合と，�A外側にある場合について，(1)式が成り立つことを示す．ただし，点電荷からの電場ベクトルは，�@の場合は1回のみ，�Aの場合は2回のみ曲面と交わるものとする．

�@[点電荷 ${\displaystyle Q}$ が ${\displaystyle S}$ の内側にある（電場ベクトル ${\displaystyle E}$ は ${\displaystyle S}$ と1回だけ交わる）とき]

�A[点電荷 ${\displaystyle Q}$ が ${\displaystyle S}$ の外側にある（電場ベクトル ${\displaystyle E}$ は ${\displaystyle S}$ と2回だけ交わる）とき]

�@と�Aの議論を用いると，1つの点電荷 ${\displaystyle Q}$ と任意の閉曲面 ${\displaystyle S}$ の場合について，以下のようにガウスの法則を示すことができる．

[1つの点電荷と任意の閉曲面の場合]

電場についての重ね合わせの原理を用いると，より一般に多数の点電荷がある場合や，電荷が連続的に分布する場合にもガウスの法則が成り立つことが分かる．

[多数の点電荷がある場合]

[電荷が連続的に分布している場合]

ホーム>>カテゴリー分類>>電磁気学>>ガウスの法則

学生スタッフ作成

2024年3月11日