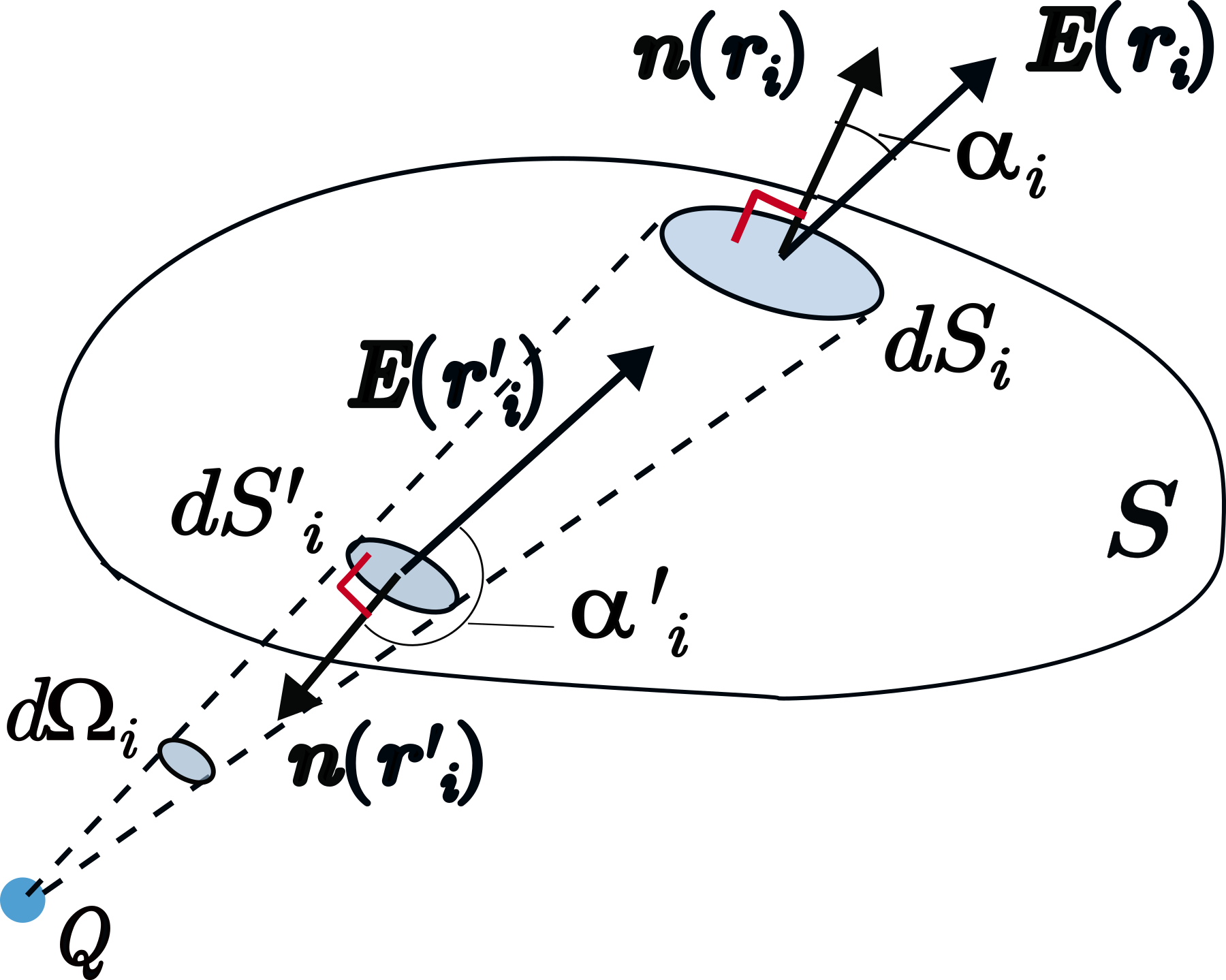
点電荷が閉曲面の外側にある場合のガウスの法則

[点電荷 ${\displaystyle Q}$ が曲面 ${\displaystyle S}$ の外側にある(電場と曲面が2回だけ交わる)場合]

閉曲面 ${\displaystyle S}$ 上で，点電荷 ${\displaystyle Q}$ から見た同一立体角 ${\displaystyle d{\Omega }_i}$ 内にある微小面積 ${\displaystyle d{S}_i}$ と ${\displaystyle d{S}_i{}^{\prime }}$ を考える．①で行った議論と同様に， ${\displaystyle d{S}_i}$ の領域について(1)式の左辺の面積分への寄与を考えると，

${\displaystyle E\left(r_i\right)\cdot n\left(r_i\right)d{S}_i=\left|E\left(r_i\right)\right|\cos {\alpha }_{i}d{S}_i}$

${\displaystyle \phantom{E\left(r_i\right)\cdot n\left(r_i\right)d{S}_i}=\frac{Q}{4\pi {\epsilon }_0}\frac{\cos {\alpha }_i}{r_i^2}d{S}_i}$

${\displaystyle \phantom{E\left(r_i\right)\cdot n\left(r_i\right)d{S}_i}=\frac{Q}{4\pi {\epsilon }_0}d{\Omega }_i}$

である． ${\displaystyle d{S}_i{}^{\prime }}$ についても同様に考えると，

${\displaystyle E\left(r_i{}^{\prime }\right)\cdot n\left(r_i{}^{\prime }\right)d{S}_i{}^{\prime }=\left|E\left(r_i{}^{\prime }\right)\right|\cos {\alpha }_i{}^{\prime }d{S}_i{}^{\prime }}$

${\displaystyle \phantom{E\left(r_i{}^{\prime }\right)\cdot n\left(r_i{}^{\prime }\right)d{S}_i{}^{\prime }}=\frac{Q}{4\pi {\epsilon }_0}\frac{\cos {{\alpha }_i}^{\prime }}{{r^{\prime }}_i^2}d{S}_i{}^{\prime }}$

である．ここで， ${\displaystyle E\left({r_i}^{\prime }\right)}$ と ${\displaystyle {r_i}^{\prime }}$ の方向に注意して①の議論を用いると， ${\displaystyle \cos \left(\pi -{{\alpha }_i}^{\prime }\right)d{S}_i{}^{\prime }={{r_i}^{\prime }}^{2}d{\Omega }_i}$ が得られる．これを上の式に用いると，

${\displaystyle E\left(r_i{}^{\prime }\right)\cdot n\left(r_i{}^{\prime }\right)d{S}_i{}^{\prime }=-\frac{Q}{4\pi {\epsilon }_0}d{\Omega }_i}$

したがって，

${\displaystyle E\left(r_i\right)\cdot n\left(r_i\right)d{S}_i+E\left(r_i{}^{\prime }\right)\cdot n\left(r_i{}^{\prime }\right)d{S}_i{}^{\prime }=0}$

となり，同一立体角 ${\displaystyle d{\Omega }_i}$ 内の2つの微小領域からの寄与が打ち消しあうことが分かる．すべての微小立体角について同様に和を取り，分割数が大きい極限を考えれば，

${\displaystyle {\displaystyle {\oint }_{S}E\left(r\right)}\cdot dS=0}$

となるので，(1)式が成り立つ．

ホーム>>カテゴリー分類>>電磁気学>>ガウスの法則>>点電荷が閉曲面の外側にある場合のガウスの法則

学生スタッフ作成

2024年3月11日