ビオ・サバールの法則 (Biot-Savart's Law)
太さの無視できる導線に定電流 が流れているとする(図1).この導線上の微小区間 (電流の流れる向きを向いた線素ベクトル)を考えると,この区間を流れる電流によって導線の周りの点 に作られる磁場 は,・・・・・・(1)
で与えられる.ここで, は微小区間 を原点としたときの点 の位置ベクトル, , は真空の透磁率である.(1)式は,ビオ・サバールの法則と呼ばれる.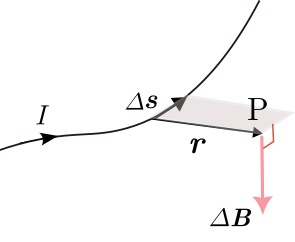
図1
次に,導線を流れる電流全体による磁場 を考える.空間内の原点 を考え,導線上の点の位置ベクトルを で表すとする(図2).(1)式を用いると,位置 における微小区間 を流れる電流が作る磁場は,
・・・・・・(2)
と表される.したがって,位置ベクトル の点 における磁場 は,(2)式を導線全体にわたって線積分することで,・・・・・・(3)
となる.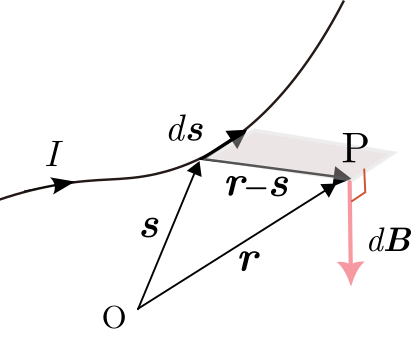
図2
線上を流れる電流ではなく,より一般的な定電流分布による磁場を考える場合は,(2)式の電流要素 を に置き換える.ここで, は位置 における電流密度, は微小体積要素である.こうして得られる を,電流密度が存在する領域にわたって体積積分することで,
・・・・・・(4)
が得られる.ホーム>>カテゴリー分類>> 電磁気学 >>ビオ・サバールの法則
学生スタッフ作成
2025年4月16日