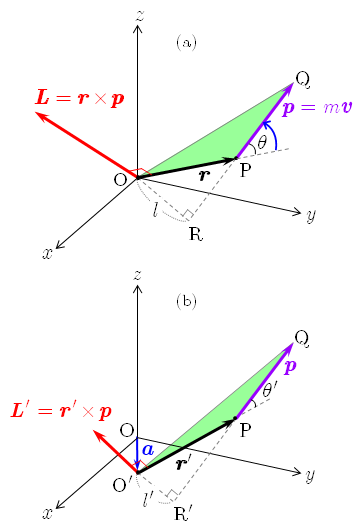
角運動量 ： 異なる座標原点 (different origin)

角運動量の定義には質点の位置ベクトルが関与しているので，一般には，位置ベクトルの始点が異なれば，質点の運動量が同じであっても角運動量は(大きさも方向も)異なる． つまり，角運動量は座標原点の選び方に依存する．

運動量 p をもつ質点が点 P にあるとする．点 O から点 P に引いた位置ベクトルを r ，点 O からベクトル a だけ隔てた点 O' から点 P に引いた位置ベクトルを r′ とすると，

r= r′ +a     - - - (1)

の関係がある．このとき，点 O のまわりの質点の角運動量は

L =r × p     - - - (2)

であり（ 図(a) ），点 O' のまわりの質点の角運動量は

L′ =r′ × p     - - - (3)

である（ 図(b) ）．この図において，点 O から直線 PQ に下ろした垂線の長さ

l= |r| sinθ

は，点 O' から下ろした垂線の長さ

l′= |r′| sinθ′

と比べると， l>l′ なので，各々の角運動量の大きさ L=lp ， L′ = l′p について， L>L′ となり，点 O のまわりの角運動量の大きさ L は点 O' のまわりの角運動量の大きさ L′ に比べて大きい．角運動量の大きさは回転運動の勢いを表す量といえるので，図の質点の運動を回転運動として考えたときには，同じ運動量 p であっても，点 O' のまわりの回転よりも点 O のまわりの回転の方が勢いが大きいということである．

式(1)を式(2)に代入し，式(3)を用いると， L と L′ の関係は

L= ( r′ +a ) ×p = r′ ×p + a×p = L′ + a×p     - - - (4)

である．

ホーム>>カテゴリー分類>>力学>>運動>>角運動量>>異なる座標原点