角運動量 (angular momentum)
質量
である(成分表示).この運動量のモーメント
角運動量は物体の回転運動において重要な概念であり,簡単にいえば回転運動の勢いを表す量である.
※ ただし,回転運動していなくても角運動量がゼロとは限らない.
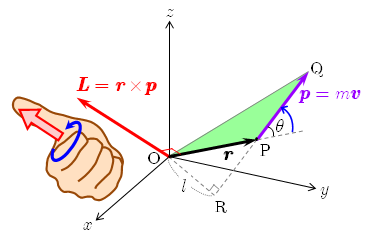
図のように,運動量
と表される.点 O から PQ を通る直線に下ろした垂線の長さ

質量
である(成分表示).この運動量のモーメント
角運動量は物体の回転運動において重要な概念であり,簡単にいえば回転運動の勢いを表す量である.
※ ただし,回転運動していなくても角運動量がゼロとは限らない.
図のように,運動量
と表される.点 O から PQ を通る直線に下ろした垂線の長さ