ベクトルのモーメント (moment of vector)

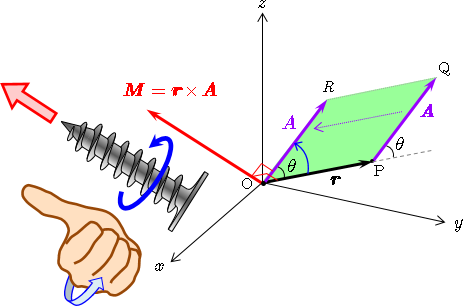
点 ${\displaystyle \text{P}}$ を始点としたベクトル ${\displaystyle \mathit{A}}$ があり，点 ${\displaystyle \text{O}}$ から引いた点 ${\displaystyle \text{P}}$ の位置ベクトルを ${\displaystyle \mathit{r}}$ とすると，ベクトル ${\displaystyle \mathit{A}}$ の点 ${\displaystyle \text{O}}$ のまわりのモーメントとは

${\displaystyle \mathit{M}=\mathit{r}\times \mathit{A}}$     - - - (1)

で定義されるベクトル量である．上式のようにベクトル ${\displaystyle \mathit{r}}$ と ${\displaystyle \mathit{A}}$ のベクトル積(外積)で定義されるので， ${\displaystyle \mathit{A}}$ の始点を ${\displaystyle \text{O}}$ に平行移動し， ${\displaystyle \mathit{r}}$ からその平行移動した ${\displaystyle \mathit{A}}$ に向かって ${\displaystyle \theta }$ 回転するときに右ネジが進む方向が ${\displaystyle \mathit{M}}$ の方向であり， ${\displaystyle \mathit{r}}$ と ${\displaystyle \mathit{A}}$ で張られる平行四辺形 ${\displaystyle \text{OPQR}}$ （淡緑の面）に垂直である．図のように右手を握りこむ向きを回転の向きにとると，右ネジの進む方向は親指の方向に対応する．ベクトルのモーメントを図示する場合，通常，図のように点 O を始点としたベクトルで表す(位置ベクトル ${\displaystyle \mathit{r}}$ の始点をベクトルのモーメントの始点とする)．

また ${\displaystyle \mathit{M}}$ の大きさは平行四辺形 ${\displaystyle \text{OPQR}}$ の面積に等しく

${\displaystyle \left|\mathit{M}\right|=\left|\mathit{r}\right|\left|\mathit{A}\right|\sin \theta }$     - - - (2)

となる．

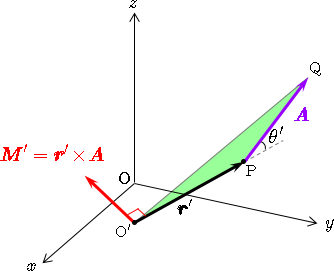
このように，ベクトルのモーメントは，そのベクトルの始点の位置に依存するため，同じベクトル量でも位置が異なればそのモーメントは異なるものになる．また，点 ${\displaystyle \text{O}}$ とは異なる点 ${\displaystyle {\text{O}}^{\prime }}$ から点 ${\displaystyle \text{P}}$ に引いた位置ベクトルを ${\displaystyle {\mathit{r}}^{\prime }}$ とすると，ベクトル ${\displaystyle \mathit{A}}$ の点 ${\displaystyle {\text{O}}^{\prime }}$ のまわりのモーメントは

${\displaystyle {\mathit{M}}^{\prime }={\mathit{r}}^{\prime }\times \mathit{A}}$     - - - (3)

となり，どの点のまわりのモーメントを考えるかによってベクトルのモーメントは異なるものになる．通常，ベクトルのモーメントの概念が出てくるのは回転運動を取り扱う場合であり，回転中心のまわりのモーメントを考えることが多い．

ホーム>>カテゴリー分類>>物理数学>>線形代数>>ベクトルのモーメント