ヘヴィサイドの階段関数 (Heaviside step function)
実数 に対して,負の値 では となり,正の値 では となる関数を,ヘヴィサイドの階段関数 (Heaviside step function) ,または単位階段関数 (unit step function) といい,以下ように表される.
--- (1)
の他にも, や で表されることもある.
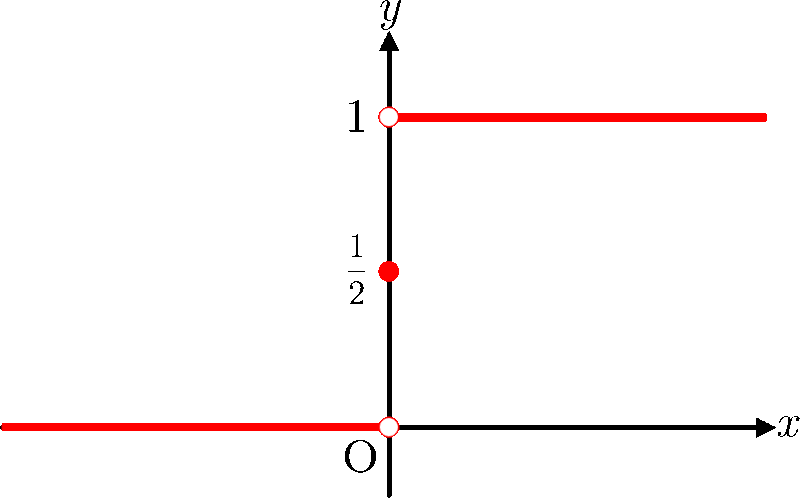
ヘヴィサイドの階段関数 のグラフ
での関数値を として,階段関数を以下のように不連続関数として定義することがある.
--- (2)
の値としては, がよく用いられる.
ヘヴィサイドの階段関数は,制御理論や信号処理においてよく用いられ,指定された時刻にスイッチが入り,その後はスイッチが入ったままの信号を表す.元々は,電気信号をモデル化するためにオリバー・ヘヴィサイド [Oliver Heaviside](イギリスの電気技師・物理学者,1850-1925)により導入された.