1�����X�e�b�v�|�e���V�����ɑ���V�����f�B���K�[�������̒����i�X�e�b�v�|�e���V�����j
1�����i ����j�̃|�e���V���������^�����鎿�� �̗ʎq�ɑ���V�����f�B���K�[�������͎����ƂȂ�D
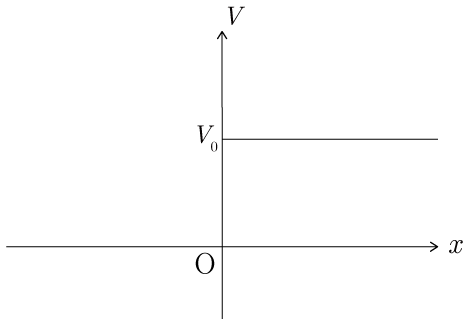
Figure1�̂悤���X�e�b�v�|�e���V����
�ɂ����āC �̏\������ �̗��q�����炠��^���ʂ������q�� �̐��̌����ɓ��˂������Ă�����l���C���̒����(�m�����x�̋�ԕ��z�������Ɉ˂炸�ω����Ȃ����)�ɂ��ẴV�����f�B���K�[�������̉������߂�D
���q�̃G�l���M�[ �����̒���Ԃ̏ꍇ�C�V�����f�B���K�[�������̉��͕ϐ������` �ŕ\�����Ƃ��ł�(�ϐ�����)�C���Ԃ��܂܂Ȃ��V�����f�B���K�[������
������(1)
���l���邱�Ƃ��ł���D�����ŁC�g�����̎��Ԉˑ����� �ł���D ���� �Ɖ��肵�āC(1)�ɑ������ƁC
[�T]
�̂Ƃ�
���C
�d�ˍ��킹�̌������C
������(2)
�ǂ���ɐi�ޔg���́C �ˑ��̔g�����܂Ŋ܂߂čl���Ȃ��ƕ�����Ȃ��D
����(2)�� �͓��˔g�C �͔��˔g�ɑΉ�����D
[�U]
�̂Ƃ�
���C
�d�ˍ��킹�̌������C
������(3)
�X�e�b�v�|�e���V�����ɁC����( )���痱�q����˂��Ă���ꍇ�C �̗̈�ł́C���˔g�Ɣ��˔g�C �̗̈�ł́C���ߔg�݂̂̉��ɂȂ� (��(3)�� )�D���������āC���͎����ƂȂ�D
���_
�ł̋��E�������W��
�C
�C
�̊W�����߂�D
�V�����f�B���K�[��������2�K�̔����������Ȃ̂ŁC���̉���1�������͑S�̈�ŘA���łȂ���Ȃ�Ȃ��D
�g����
�͌��_
�œ������Ȃ邽��
������(4)
�܂��C����
�͌��_ �œ������Ȃ邽��
������(5)
(4) (5) ���
�������C���� ����(4)�ɑ������
��������D����āC�W�� �C �� ��p����
�C
�ƕ\����D������
�C
[1]
�̏ꍇ
���˔g�̃G�l���M�[���|�e���V�����̃G�l���M�[���傫���Ƃ��C
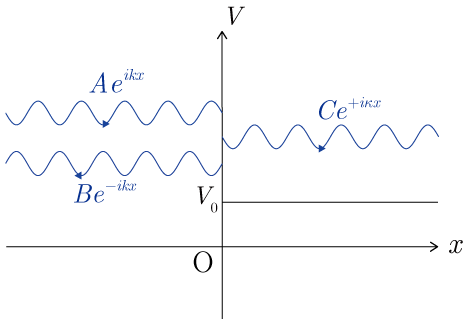
�͎����ɂȂ�D���������āC���˔g �̈ꕔ�͔��˂�(���˔g )�C�ꕔ�͓��ߔg �Ƃ��āC �̗̈�ɓ`������(Figure2)�DFigure1�ɏd�˂āC�g�����̎�����g���Ŏ������D�c���̓G�l���M�[�C������1�������W�� ���������D
[2]
�̏ꍇ
���˗��q�̃G�l���M�[
���|�e���V�����̃G�l���M�[
��菬�����Ƃ��C
�͋����ɂȂ�D���ߔg��
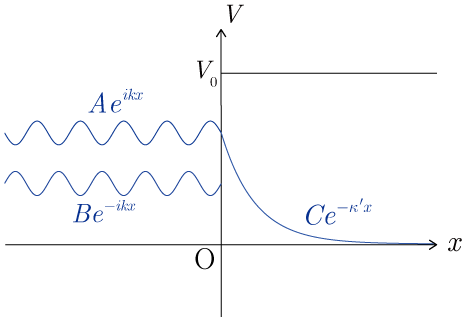
�Ƃ��āC �̗̈�Ŏw�����I�Ɍ�������D���������āC���˔g �́C �̗̈�ɂ����Ďw�����I�Ɍ�������(Figure3)�D���̐}�ł��C�g�����̎�����j���Ŏ������D
�z�[��>>�J�e�S���[���� >>�ʎq�͊w>>1�����X�e�b�v�|�e���V�����ɑ���V�����f�B���K�[�������̒����i�X�e�b�v�|�e���V�����j
�w���X�^�b�t�쐬
2025�N8��5��