斜面を転がる剛体球
ある球(質量
,半径
,慣性モーメント
)が,水平からなす角
の斜面の上を転がりながら落下した(図1).球がざらざらした斜面から受ける摩擦力を
,垂直抗力を
,球の重心の加速度を
,回転の角加速度を
,重力加速度の大きさを
とする.
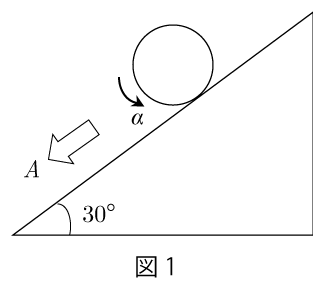
球に作用する力を図1にすべて書け.
解答
重心の運動方程式を書け(これを①とする).
解答
解説
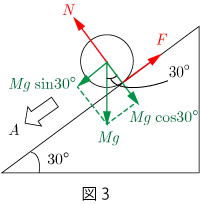 球にはたらく重力を加速度の方向と,それに垂直な方向とに分解すると図3のようになる.
球にはたらく重力を加速度の方向と,それに垂直な方向とに分解すると図3のようになる.
加速度の方向に働く力は
と
である.
よって運動方程式はになる.
閉じる
回転運動の方程式を書け(これを②とする).
解答
解説
回転運動の方程式は,
で与えられ,
はトルク
である.トルクとは,物体に回転運動を生じさせる回転軸の周りの力のモーメントのことで,今の場合
である.
閉じる
③
を用いて,設問,の解答の2式①②から
と
を消去して球の重心の加速度
を求めよ.
解答
閉じる
解説
②,③から
を消去して
これを①に代入して
閉じる
球の慣性モーメント
・・・④
を用いて,球の重心の加速度
を数値と
だけを用いて表せ.
解答
解説
閉じる
球が回転しないで斜面を滑った場合と,球が回転して斜面を転がった場合では,どちらがはやく落下するか.適切な選択肢を選べ.
球が回転しないで斜面を滑った場合
球が回転して斜面を転がった場合
どちらも同じ
球が回転しない場合を考える.このとき
だから,②より
となり,である.これを①に代入すると
となり,
である.
これは
より大きいので答えは
「球が回転しないで斜面を滑った場合」
である.
閉じる
参照:斜面を滑らず転がり落ちる剛体球の運動
ホーム>>物理演習問題>>力学>>剛体の力学>>剛体の平面運動>>斜面を転がる剛体球
学生スタッフ作成
最終更新日:2025年9月17日
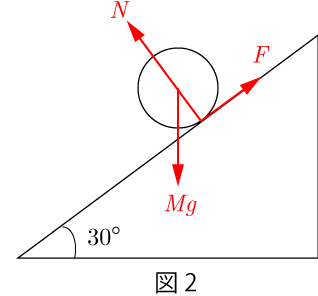
 球にはたらく重力を加速度の方向と,それに垂直な方向とに分解すると図3のようになる.
球にはたらく重力を加速度の方向と,それに垂直な方向とに分解すると図3のようになる.