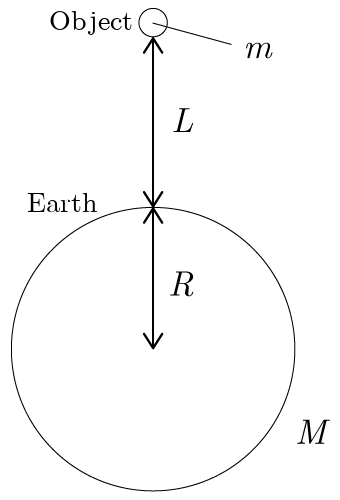
万有引力によるポテンシャルエネルギー
図のように地球表面（地表）から距離
L
の高さまで質量
m
の物体を引き上げることを考える．ここで，地球を質量
M
，半径
R
の球とみなす．距離
r
だけ離れた，質量
m
1
，
m
2
の2つの物体の間には大きさ
F(
r
)=G
m
1
m
2
r
2
の
万有引力が働く．ここで，
G
は万有引力定数である．地球の質量
M
は物体の質量
m
に比べて非常に大きいため，地球は静止したままであるとし，空気の影響は無視できるものとする．
(1)
地表で静止していた物体に力を加えて，地表から距離
L
の高さまで物体をゆっくり引き上げたとき，その力のした仕事
W
を求めよ．
解答
解説
W=
∫
R
R+L
F(
r
)dr
=
∫
R
R+L
G
Mm
r
2
dr
=
[
−G
Mm
r
]
R
R+L
=−G
Mm
R+L
+G
Mm
R
=
GMmL
R(
R+L
)
閉じる
(2)
地表から距離
L
の高さまで物体を引き上げた後，物体を放して初速ゼロで自由落下させた．地表に達する直前の物体の速さを求めよ．
解答
解説
(
1
)
で求めた仕事は，物体が地表にあるときを基準点として，物体が地表から高さ
L
の位置にあるときの系のポテンシャルエネルギーである．従って，
力学的エネルギー保存の法則
を用いて
1
2
m
v
2
=
GMmL
R(
R+L
)
より，地表に達する直前の物体の速さは
v=
2GML
R(
R+L
)
と求まる．
閉じる
(3)
この物体を地面から初速
v
で打ち上げる．物体が地球の重力圏から脱出するための初速
v
の条件を求めよ．
解答
解説
無限遠を基準点としたとき，物体が地表にあるときの系のポテンシャルエネルギーは
U=−
∫
R
∞
G
Mm
r
2
dr
=
[
G
Mm
r
]
R
∞
=−G
Mm
R
である．物体が地球の重力圏から脱出するためには，無限遠に達したときの速さ
v
∞
がゼロより大きければよい．したがって，力学的エネルギー保存の法則より
1
2
m
v
2
−G
Mm
R
=
1
2
m
v
∞
2
>0
であればよい．したがって，
v>
2GM
R
となる．
閉じる
ホーム>>物理演習問題>>力学>>仕事・エネルギー>>エネルギー>>万有引力によるポテンシャルエネルギー
学生スタッフ作成
2021年1月18日
