力学的エネルギー保存の法則 (law of conservation of mechanical energy)

運動エネルギー ${\displaystyle K〔\text{J}〕}$ と位置エネルギー ${\displaystyle U〔\text{J}〕}$ （重力による位置エネルギー，弾性力による位置エネルギーなど）との和を力学的エネルギー (mechanical energy)という．物体に作用する力が保存力のみの場合，または保存力以外の力が仕事をしない場合，力学的エネルギーは一定に保たれる．これを力学的エネルギー保存の法則 (law of conservation of mechanical energy)といい，

${\displaystyle K+U=\text{const}}$

と表される．位置エネルギー ${\displaystyle U}$ は一般に物体の位置 ${\displaystyle \overrightarrow{r}〔\text{m}〕}$ の関数であり，主に重力による位置エネルギーか弾性力による位置エネルギー，もしくはその両方を含む．

例えば，ばね定数 ${\displaystyle k〔\text{N/m}〕}$ のばねにつながった質量 ${\displaystyle m〔\text{kg}〕}$ の物体が速さ ${\displaystyle v〔\text{m/s}〕}$ で運動している状況を考える．このとき，運動エネルギーは ${\displaystyle K=\frac{1}{2}m{v}^2}$ であり，重力による位置エネルギーの基準点から測った物体の位置の高さを ${\displaystyle h〔\text{m}〕}$ ，ばねの自然長からの変位を ${\displaystyle x〔\text{m}〕}$ とすると，位置エネルギーは ${\displaystyle U=mgh+\frac{1}{2}k{x}^2}$ となるので

${\displaystyle \frac{1}{2}m{v}^2+mgh+\frac{1}{2}k{x}^2=\text{const}}$

が成り立つ．ここで， ${\displaystyle g〔{\text{m/s}}^{\text{2}}〕}$ は重力加速度の大きさである．

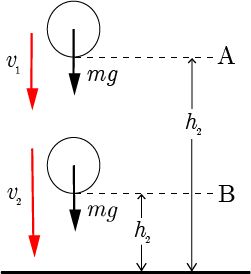
図のように，質量 ${\displaystyle m〔\text{kg}〕}$ の物体が自由落下(Free fall)するとき，高さAの位置と高さBの位置での力学的エネルギー ${\displaystyle E_{\text{A}}}$ , ${\displaystyle E_{\text{B}}}$ はそれぞれ

${\displaystyle E_{\text{A}}=K_{\text{A}}+U_{\text{A}}=\frac{1}{2}m{v}_1^2+mg{h}_1}$

${\displaystyle E_{\text{B}}=K_{\text{B}}+U_{\text{B}}=\frac{1}{2}m{v}_2^2+mg{h}_2}$

であるので，力学的エネルギー保存の法則より ${\displaystyle E_{\text{A}}=E_{\text{B}}}$ なので，

${\displaystyle \frac{1}{2}m{v}_1{}^2+mg{h}_1=\frac{1}{2}m{v}_2{}^2+mg{h}_2}$

が成り立つ．

上式について仕事と運動エネルギーの関係を用いて考えると，高さ ${\displaystyle \text{A}}$ の位置から高さ ${\displaystyle \text{B}}$ の位置まで，重力が物体にする仕事は

${\displaystyle W=mg(h_1-h_2)}$

で，この分だけ運動エネルギーが増加するので

${\displaystyle mg(h_1-h_2)=\frac{1}{2}m{v}_2{}^2-\frac{1}{2}m{v}_1{}^2}$

が成り立つ．よって

${\displaystyle \frac{1}{2}m{v}_1{}^2+mg{h}_1=\frac{1}{2}m{v}_2{}^2+mg{h}_2}$

が得られる．

ホーム>>物理基礎>>第1編 物体の運動とエネルギー>>第3章　仕事と力学的エネルギー>>力学的エネルギー保存の法則

最終更新日2025年9月24日