保存力 (conservative force)
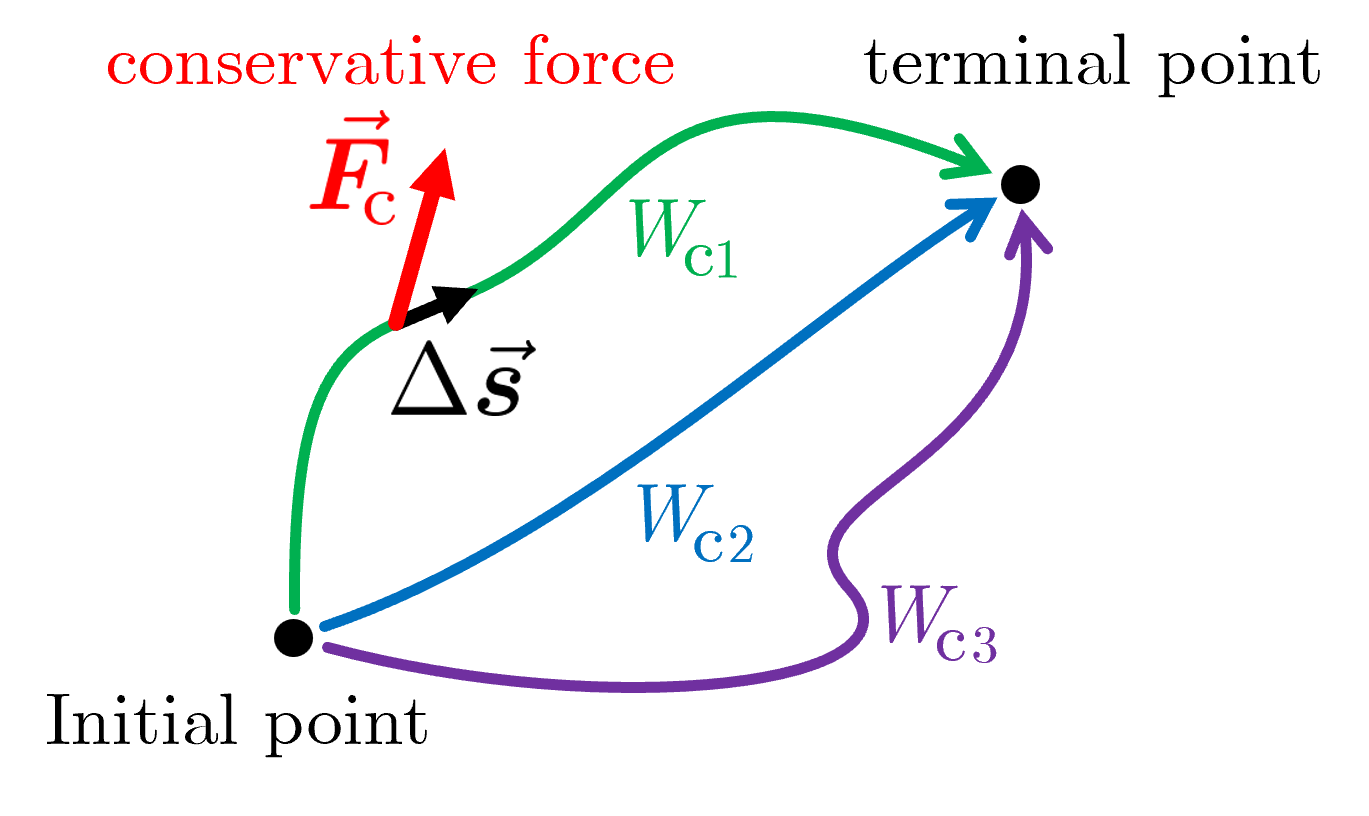
図1 保存力のする仕事
物体に力を加えて移動させるとき,その力のする仕事が物体のたどる経路に関係なく,どの経路をたどっても同じ場合(つまり,経路の始点 (initial point) と終点 (terminal point) の位置のみで仕事が決まる場合),その力を保存力 (conservative force) という.位置エネルギーは保存力のする仕事により定義される(下記参照).
図1に示すように,物体に保存力 を加えて始点から終点まで3つの経路で移動させる場合,各経路における保存力のする仕事をそれぞれ , , とすると,これらの仕事は経路によらず
が成り立つ.また,物体に保存力を加えて移動させた経路の始点と終点が同じ(閉じた経路)であれば,その保存力のした仕事はゼロである.
保存力には,重力(万有引力),ばねの弾性力,静電気力,磁気力などがある.一方,保存力ではない力(非保存力)には,動摩擦力や空気抵抗などがある.
保存力のする仕事の例
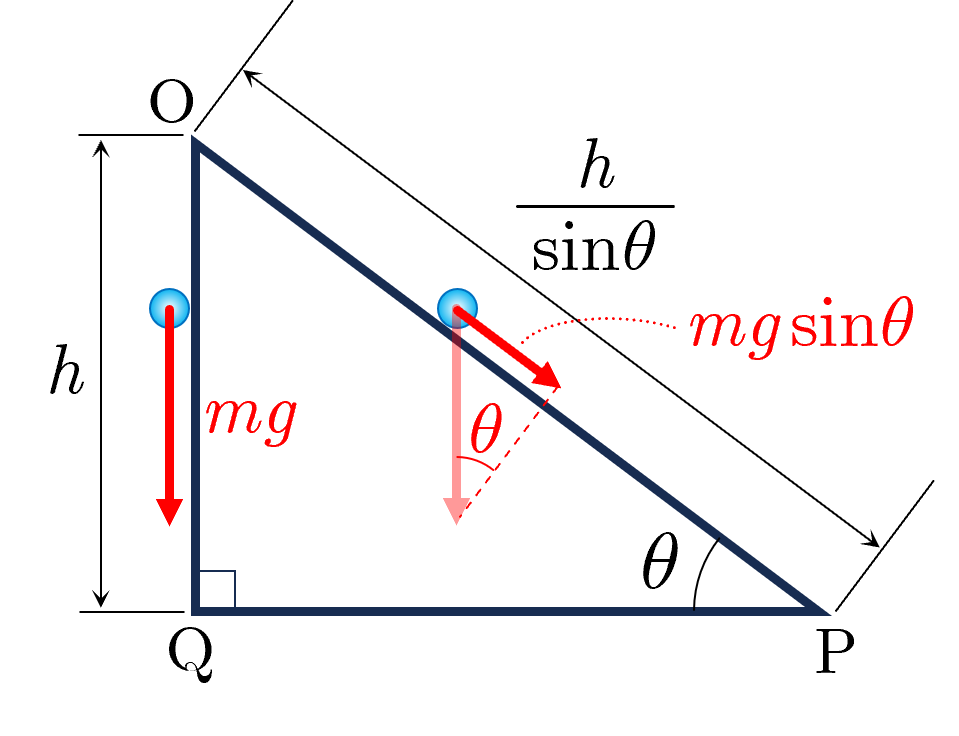
図2 異なる2経路での重力のする仕事
保存力のする仕事の例として,図2に示すような水平面に固定された傾斜角 ,高さ の斜面台において,質量 の小球が斜面上端の点 から斜面下端の点 に移動するときの,小球にはたらく重力のする仕事を考える.重力加速度の大きさを とすると,斜面に沿って点 から点 まで移動する経路では,小球にはたらく重力の斜面方向成分が であり,移動距離が なので,重力のする仕事は
である.一方,点 から鉛直下向きにある点 を経由して点 まで移動する経路では,点 から点 までの重力のする仕事が で,点 から点 までの重力のする仕事はゼロであるので,全仕事は
である.よって,これら2つの経路で重力のする仕事は変わらない.
保存力と位置エネルギーの関係
ある点における位置エネルギーは,保存力がその点から基準点までにする仕事により定義される.例えば,質量 の物体が地面から高さ の位置にあるときの重力による位置エネルギー は,物体にはたらく重力が高さ の位置から地面までに物体にする仕事 となる( は重力加速度の大きさ).
ホーム>>物理基礎>>第1編 物体の運動とエネルギー>>第3章 仕事と力学的エネルギー>>保存力
最終更新日2025年9月24日