剛体のつり合い条件(1次元)

剛体(Rigid body)にはたらく力のつり合いでは，並進運動しないための条件である「物体にはたらく力の和 ${\displaystyle =\overrightarrow{0}}$ 」に加えて，回転し始めないための条件である「力のモーメント の和 ${\displaystyle =0}$ 」が必要である．つまり，剛体のつり合いの条件 は次のようになる．

(1)力の和が ${\displaystyle \overrightarrow{0}}$ (並進運動し始めない条件)

${\displaystyle \overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\cdot \cdot \cdot =\overrightarrow{0}}$

(2)任意の点のまわりの力のモーメントの和が ${\displaystyle 0}$ (回転運動し始めない条件)

${\displaystyle M_1+M_2+M_3+\cdot \cdot \cdot =0}$

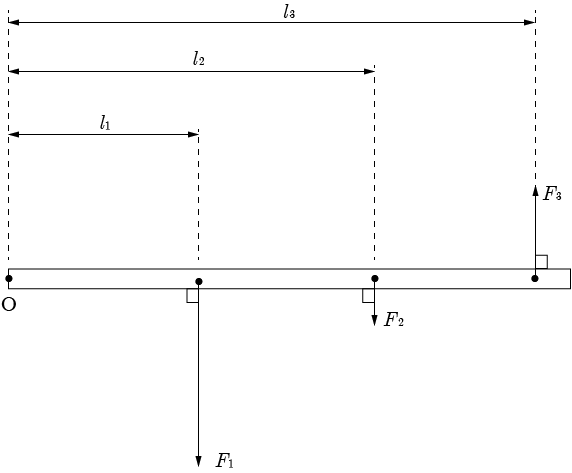
例として，下図において剛体が点Oのまわりで回転しないとする．剛体にはたらく力の大きさを ${\displaystyle F_1=\left|\overrightarrow{F_1}\right|}$ ， ${\displaystyle F_2=\left|\overrightarrow{F_2}\right|}$ ， ${\displaystyle F_3=\left|\overrightarrow{F_3}\right|}$ とすると， ${\displaystyle M_1=-F_1{l}_1}$ ， ${\displaystyle M_2=-F_2{l}_2}$ ， ${\displaystyle M_3=F_3{l}_3}$ となるので，つり合いの条件の(2)は，

$\left(-F_1{l}_1\right)+\left(-F_2{l}_2\right)+\left(F_3{l}_3\right)=0$

と表される．

また，剛体のつり合いの条件が成立しているときは，O点だけでなく，他のどの点のまわりにおいても，この式は成り立つ．

ホーム>>物理>>第1編 力と運動>>第1章 剛体>>剛体のつり合い条件(1次元)

最終更新日： 2025年9月18日