ドップラー効果 (Doppler effect)
音源
と観測者
が相対的に移動しているとき,観測者
が観測する音源
からの音の振動数
は音源本来の振動数
とは異なる現象が起きる.この現象をドップラー効果 (Doppler effect)といい,身近な例では,救急車が通り過ぎるときにサイレンの音の高さが変化して聞こえる,などがある.
ここでは,空気中の音の速さを
として,以下の場合を考える.
- 音源だけが動く(観測者は静止)場合
- 観測者だけが動く(音源は静止)場合
- 音源も観測者も動く場合
- 風が吹いている場合
- 音源または観測者が斜めに動く場合
- 反射壁(板)がある場合
1. 音源
だけが動く(観測者は静止)場合 ▲
音源
と観測者
を結ぶ直線上で,
から
への向きを正として
が速度
(
)で動いているとき,
が観測する音の振動数
は次式で与えられる.
--- (1)
▽【式(1)の導出】を閉じる
振動数
の音を発する音源
と観測者
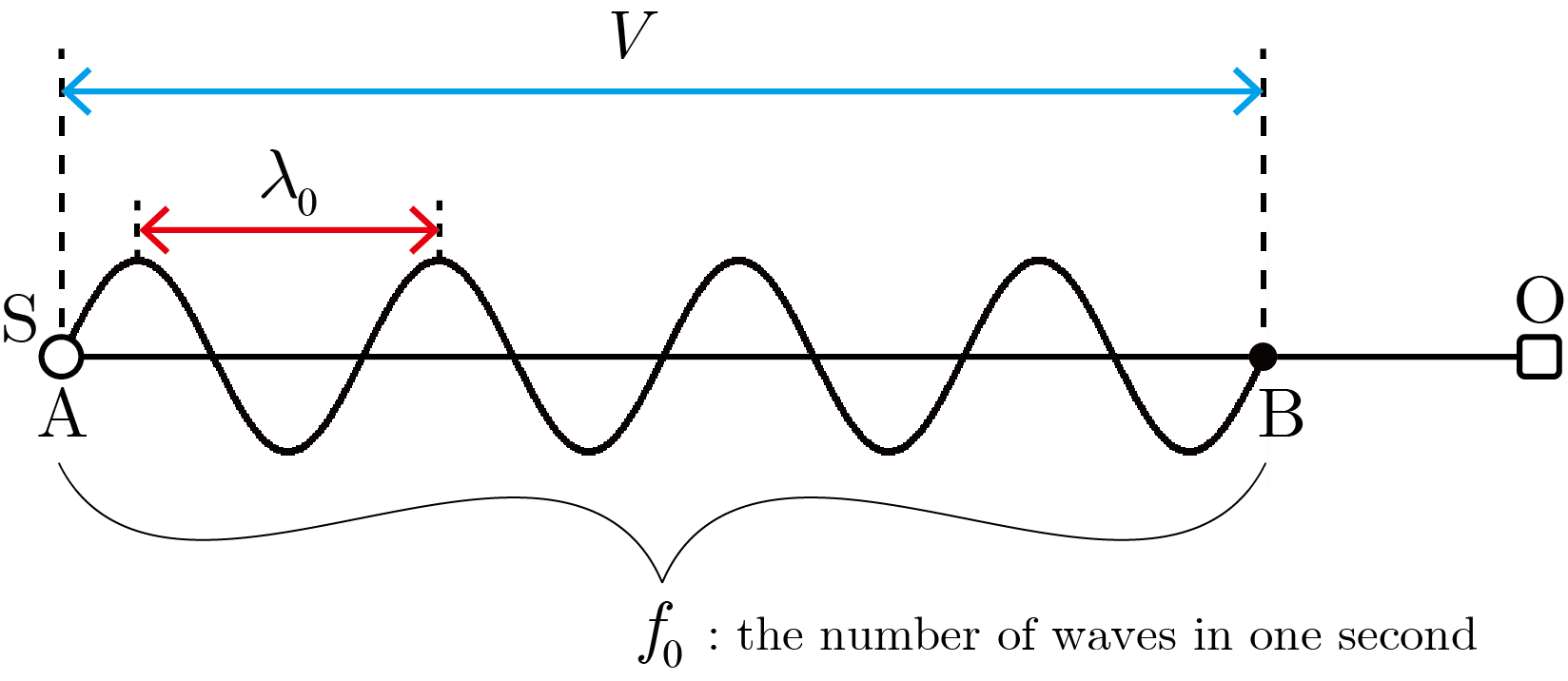
がともに静止しているとき,風は吹いていないものとすると,
から
に伝わる音の波長は
である.1波長を1つの波とすると,1秒間に音が進む距離
の間に
個の波が含まれる.
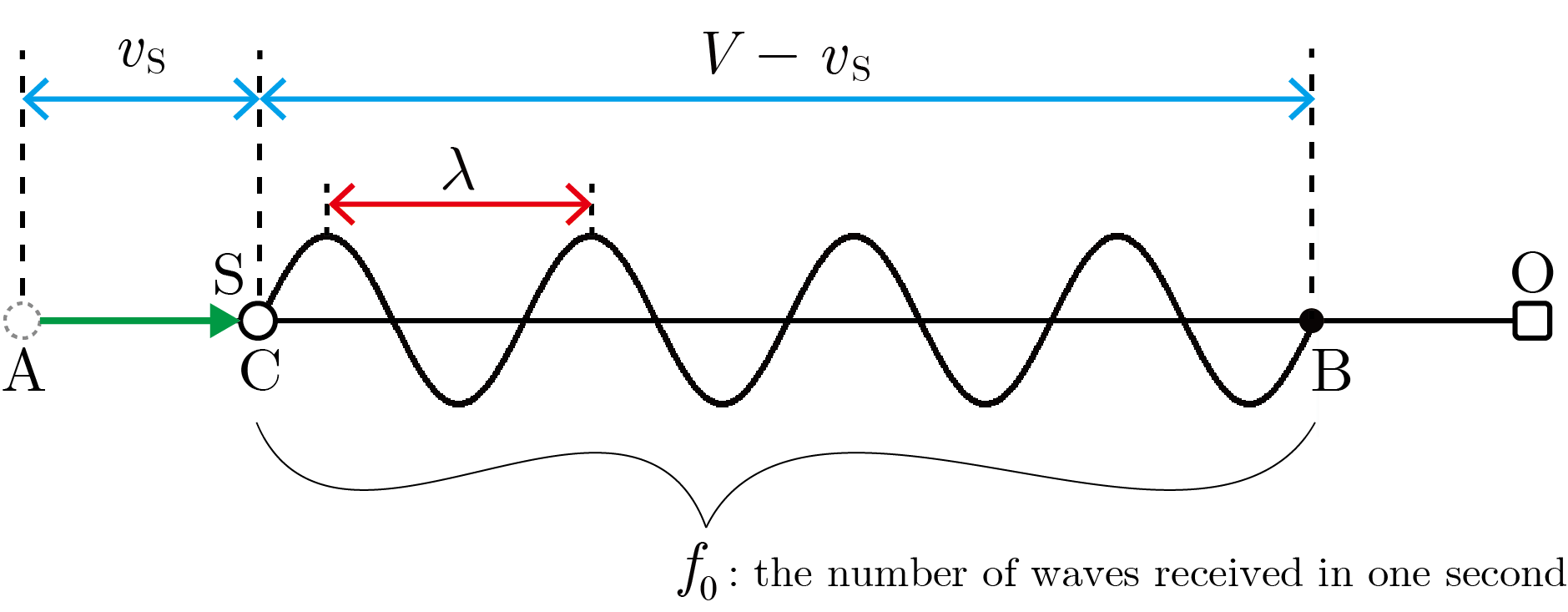
ここで,最初,点
に位置していた音源
が観測者
に向かって速度
(
)で近づく場合を考える(下図).点
で
から出た音は1秒後に点
に達し,そのとき
は点
で
番目の波を出し終える.
したがって,距離
の間に
個の波が存在するので,
が観測する音の波長は縮まって
となる.空気に対して静止している
に対して音は速さ
で通り過ぎるので,
が観測する音の振動数は
となる.よって,この場合は元の音よりも高く聞こえる.(音源
が観測者
から遠ざかる場合,式(1)において
が負の値であるので音が低くなる.)
2. 観測者
だけが動く(音源は静止)場合 ▲
音源
と観測者
を結ぶ直線上で,
から
への向きを正として
が速度
(
)で動いているとき,
が観測する音の振動数
は次式で与えられる.
--- (2)
▽【式(2)の導出】を閉じる
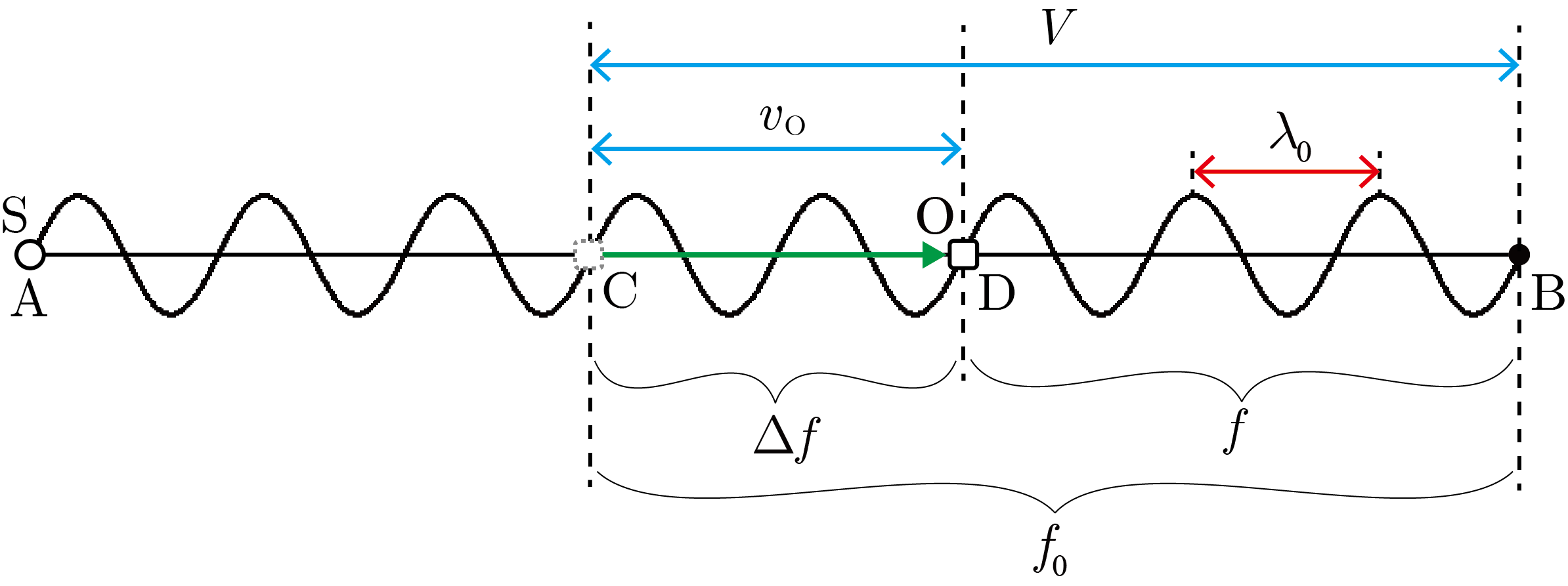
最初,点
に位置していた観測者
が点
で静止している音源
から速度
(
)で遠ざかる場合を考える(下図).
点
で
を通過した音は1秒後に
進み,その間に
は
進む.よって,
は1秒間に
(
)個の波を観測するため,
が聞く音の振動数は
となる.
より,観測者
が観測する音の振動数は
となる.よって,この場合は元の音よりも低く聞こえる.(観測者
が音源
に近づく場合,式(2)において
が負の値であるので音が高くなる.)
3. 音源
も観測者
も動く場合 ▲
音源
と観測者
を結ぶ直線上で,
から
への向きを正として
が速度
(
),
が速度
(
)で動いているとき,
が観測する音の振動数
は次式で与えられる.
--- (3)
上の(3)式において
とおくと(1)式となり,
とおくと(2)式となる.
▽【式(3)の導出】を閉じる
音源
と観測者
を結ぶ直線上で,それぞれ空気に対して速度
,
で運動している場合を考える.
は1秒間に距離
の間に
個の波を出すので,
が聞く音の波長は
となる.
は1秒間に距離
の間にある
個の波(波長
)を聞く.したがって,
となる.
4. 風が吹いている場合 ▲
音源
と観測者
を結ぶ直線に沿って,一様な風が吹いて媒質(空気)全体が一定の速さ
(
)
で動いている場合,地面に静止している立場から見ると,音は風と同じ向きには
の速さで,風と逆向きには
の速さで伝わる.
から
への向きを正として
の速度と
の速度をそれぞれ
,
とすると,
が観測する音の振動数
は次式で与えられる.
に対して
が風下の場合:
--- (4)
に対して
が風上の場合:
--- (5)
5. 音源
または観測者
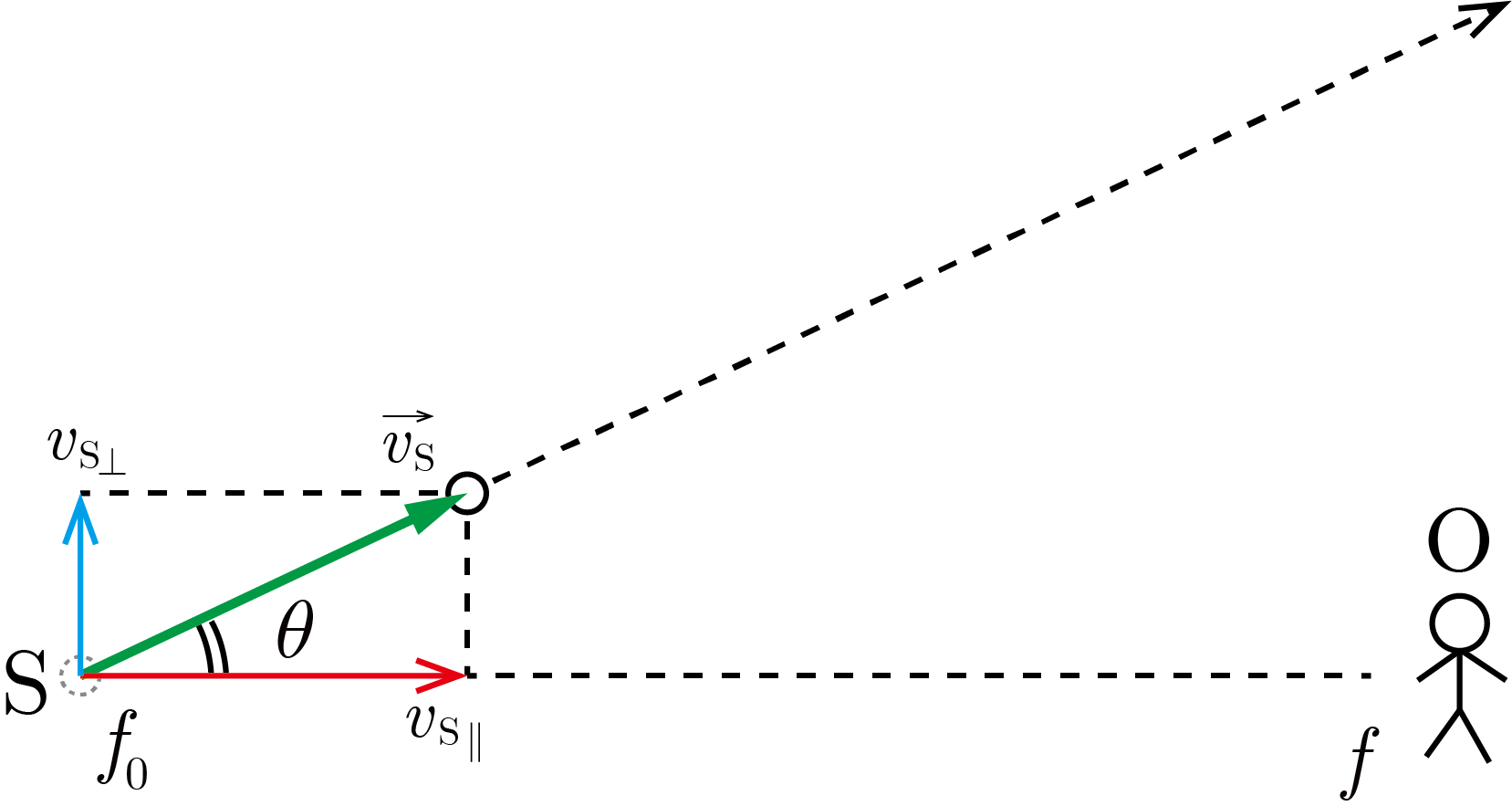
が斜めに動く場合 ▲
図のように音源
が観測者
を結ぶ直線
と角
の方向に速さ
で進む場合を考える.
の速度
を,
方向成分
(視線速度)と
方向に垂直な成分
に分解すると,ドップラー効果に効いてくるのは視線速度
のみであり,音源
のみが動く場合の式(1)から,観測者
が観測する音の振動数
は次式で与えられる.
--- (6)
観測者
が斜めに動く場合も同様で,
が直線
と角
の方向に速さ
で進む場合,速度の
方向成分
のみがドップラー効果に効く.このとき,観測者
のみが動く場合の式(2)から,観測者
が観測する音の振動数
は次式で与えられる.
--- (7)
6. 反射壁(板)がある場合 ▲
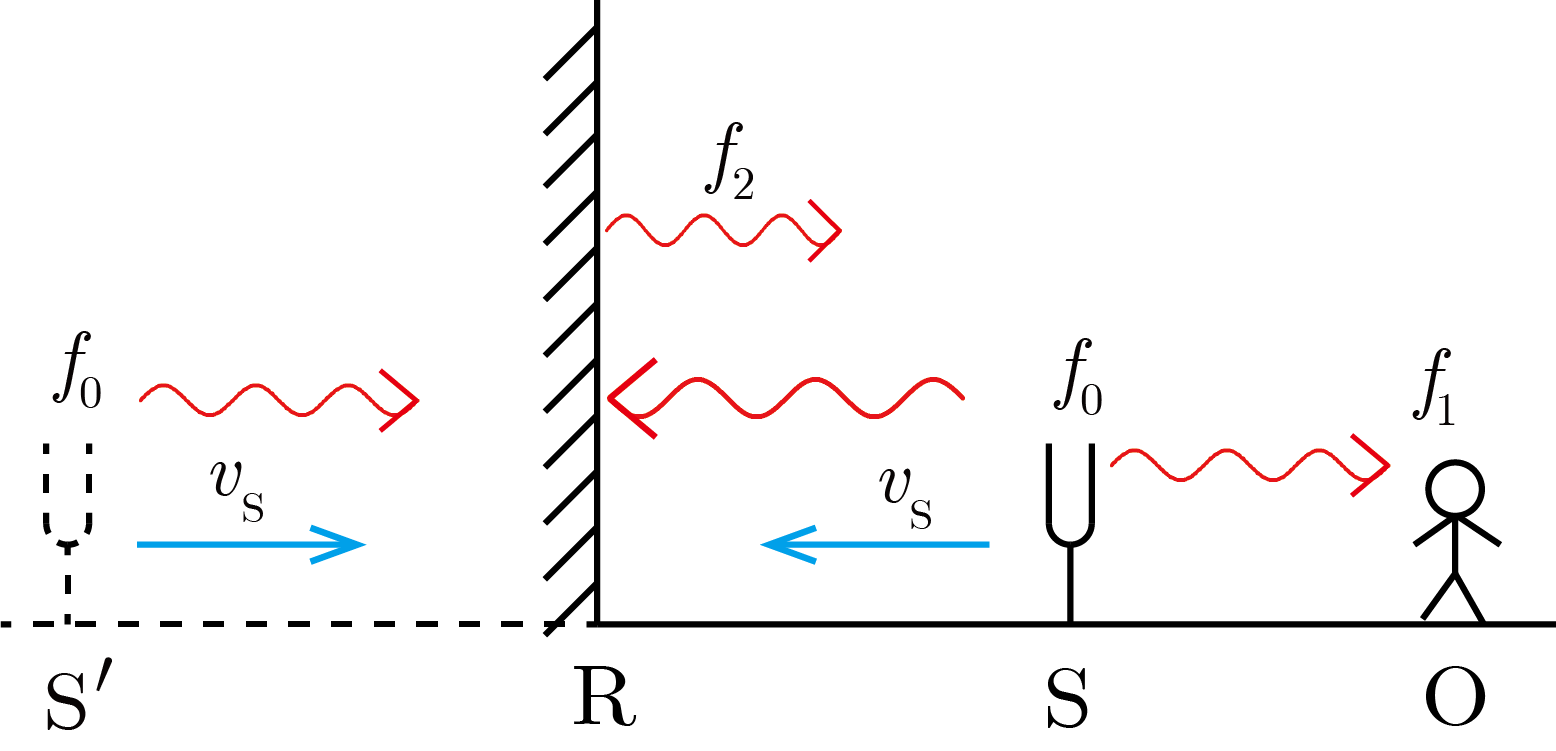
■ 静止した反射壁
に対して音源
が速さ
で動く場合
図のように反射壁
,音源
,観測者
の順に並び,直線
と
の面は垂直とする.
振動数
の音を発する
が
方向を
に向かって速さ
で近づくとき,
が
から直接聞く音の振動数
は,音源
のみが動く場合の式(1)から次式となる.
一方,壁からの反射音の振動数
は,壁を観測者と考えたときに壁が受け取る音の振動数であるので次式となる.
これは,あたかも同じ振動数の音源
が壁の向こうから
に向かって速さ
で近づいたと考えたときの
が聞く音の振動数である.このとき,
が観測する1秒間のうなりの回数
は次式で与えられる.
--- (8)
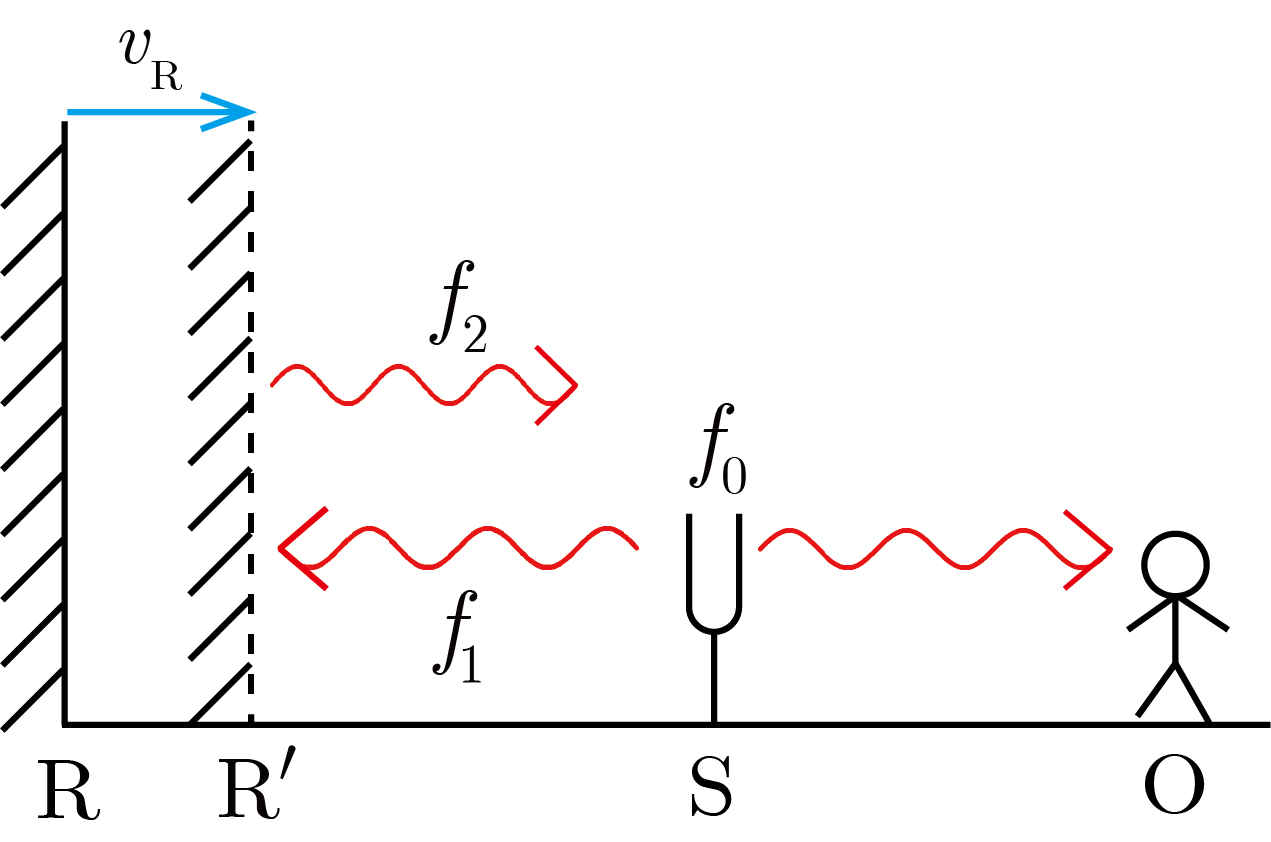
■ 静止した音源
に対し反射壁
が速度
で動く場合
図のように反射壁
,音源
,観測者
の順に並び,直線
と
の面は垂直とする.
が
方向を,振動数
の音を発する
に向かって速さ
で近づくとき,壁を観測者と考えたときに壁が受け取る音の振動数
は,観測者
のみが動く場合の式(2)から次式となる.
は受け取った音を反射する,つまり音源として観測者
に向かって発するので,
が観測する反射した音の振動数
は,音源
のみが動く場合の式(1)から次式となる.
--- (9)
このとき,
が観測する1秒間のうなりの回数
は次式で与えられる.
--- (10)
ホーム>>物理>>第3編 波>>第2章 音>>ドップラー効果
学生スタッフ作成
最終更新日:
2025年10月24日