【質問/問題】
(1)二次方程式x^2+x+k=0の2解をα，βとする．
複素数平面において3点1，α，βが正三角形の頂点になるような，定数kの値
(2)4点A,B,C,Dがこの順で四角形の頂点になっているとする．
それぞれを複素数でa,b,c,dと表す．これらが条件(a)(b)(c)を全て満たす時，
ABCDはどのような四角形となるか?
(a)a+c=b+d
(b)(b-a)/(d-a)は純虚数
(c)(a-c)^2/(a-d)(c-d)は実数
=======================================================
（1）についてですが，k=1,(1/3)となりましたが，
これは，αとβが共役であるとしてだしたのですが，（解と係数の関係より．）
共役であるといえるのは，実数係数の方程式の時だった気がします．kが複素数となる時も考えないといけないのでしょうか?

（2）についてはうまくできないです．
よろしくおねがいします．

【解答】

(1) 複素数の係数に対しても解と係数の関係は成り立つように思います．実際に解いていくと，kは実数になってしまいます．k=1/3はｔｋさんも書き込んでいるように正三角形にならないのでは．

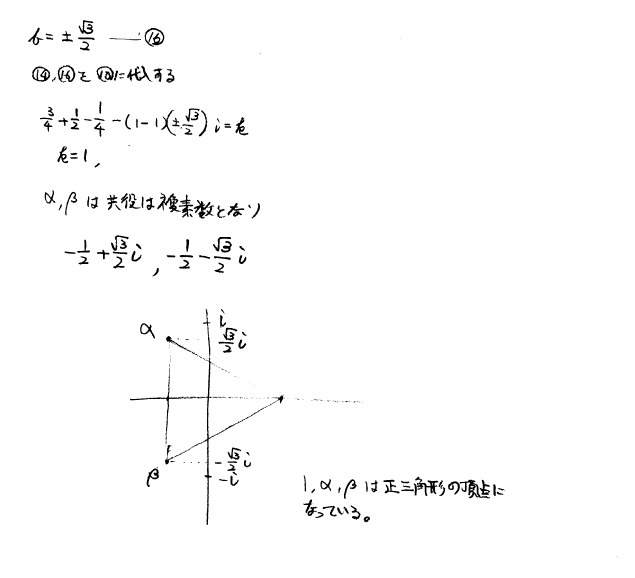
ｔｋさんのアドバイス

(2)についてですが
(a)はa-d=b-cと変形して，考えます．左辺はＤが始点でＡが終点，右辺はＣが始点，Ｂが終点のベクトルと捉えることができます．コレが等号でつながれているから，平行且つ大きさが等しいわけです．

(b)については(b-a)/(d-a)=qiとすると(b-a)=(d-a)･qi
これは「ＡＤベクトルを９０°，ｑ倍拡大回転したものがＡＢベクトルだ」ということです．

(c)は(b)を応用してできると思います．

管理人のアドバイス

KIT数学ナビゲーションの以下のページも参考にしてください．
複素数の和と差，複素数の商，直線のなす角