基底の変換 (詳細)

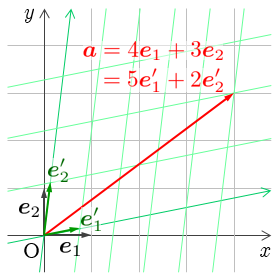
$3$\displaystyle{n}$ 次元実ベクトル空間 $3$\displaystyle{{\displaystyle{R}}^{n}}$ の任意のベクトルの成分表示

$3$\displaystyle{ \displaystyle{a}= $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ --- (1)

は基本ベクトル $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ を用いて，基本ベクトル表示

で表すことができ，(1) の表記は (2) の係数の組 $3$\displaystyle{ $ \hspace{1}{a}_{1},\text{\hspace{1}}\hspace{1}{a}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{a}_{n} $ }$ でもってベクトルを表す方法とみることができる． $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ は $3$\displaystyle{{\displaystyle{R}}^{n}}$ の基底の一つであり，ベクトル $3$\displaystyle{\displaystyle{a}}$ を別の任意の基底 $3$\displaystyle{ \{ \displaystyle{e}_{1}^{\prime },\text{\hspace{1}}\displaystyle{e}_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}\displaystyle{e}_{n}^{\prime } \} }$ を用いて同様に

$3$\displaystyle{ \displaystyle{a}=a_{1}^{\prime }\displaystyle{e}_{1}^{\prime }+a_{2}^{\prime }\displaystyle{e}_{2}^{\prime }+\cdots +a_{n}^{\prime }\displaystyle{e}_{n}^{\prime } }$ --- (3)

と表すこともできる．ここで， $3$\displaystyle{ \{ \displaystyle{e}_{1}^{\prime },\text{\hspace{1}}\displaystyle{e}_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}\displaystyle{e}_{n}^{\prime } \} }$ は正規直交基底である必要はない．このように基底を取り替えた場合，ベクトル $3$\displaystyle{\displaystyle{a}}$ を表す際に係数の組 $3$\displaystyle{ $ a_{1}^{\prime },\text{\hspace{1}}a_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}a_{n}^{\prime } $ }$ で (1) と同じ成分表示の表記を使うというのは紛らわしいので，(2) や (3) の行列表現を用いて，

$3$\displaystyle{ \displaystyle{a}=\hspace{1}{a}_{1}\hspace{1}{\displaystyle{e}}_{1}+\hspace{1}{a}_{2}\hspace{1}{\displaystyle{e}}_{2}+\cdots +\hspace{1}{a}_{n}\hspace{1}{\displaystyle{e}}_{n} }$ $3$\displaystyle{ = $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$
$3$\displaystyle{ =a_{1}^{\prime }\displaystyle{e}_{1}^{\prime }+a_{2}^{\prime }\displaystyle{e}_{2}^{\prime }+\cdots +a_{n}^{\prime }\displaystyle{e}_{n}^{\prime } }$ $3$\displaystyle{ = $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ $ \begin{array} a_{1}^{\prime } & \vspace{6}\\ a_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ a_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ --- (4)

というように，係数の $3$\displaystyle{n\times 1}$ 行列の前に基底の $3$\displaystyle{n\times n}$ 行列をかけて表すことで基底を明示し区別すると，どういう基底を用いているか分かりやすい．

基底 $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ から別の基底 $3$\displaystyle{ \{ \displaystyle{e}_{1}^{\prime },\text{\hspace{1}}\displaystyle{e}_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}\displaystyle{e}_{n}^{\prime } \} }$ への変換を行列 $3$\displaystyle{T}$ を用いて

$3$\displaystyle{ $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ = $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ \text{\hspace{1}}T }$ --- (5)

のように表すことにすると，この変換行列 $3$\displaystyle{T}$ は

$3$\displaystyle{ T={ $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ }^{ - 1 }\text{\hspace{1}} $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ --- (6)

である．今の場合， $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ は基本ベクトルなので， $3$\displaystyle{ T={E}^{ - 1 } $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ $3$\displaystyle{ = $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ となる．(4) の関係から

$3$\displaystyle{ $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ = $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ \text{\hspace{1}}T\text{\hspace{1}}{T}^{ - 1 }\text{\hspace{1}} $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ $3$\displaystyle{ = $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ $ \begin{array} a_{1}^{\prime } & \vspace{6}\\ a_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ a_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$

であるので，係数 $3$\displaystyle{ $ \hspace{1}{a}_{1},\text{\hspace{1}}\hspace{1}{a}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{a}_{n} $ }$ と係数 $3$\displaystyle{ $ a_{1}^{\prime },\text{\hspace{1}}a_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}a_{n}^{\prime } $ }$ の間に1次変換

$3$\displaystyle{ $ \begin{array} a_{1}^{\prime } & \vspace{6}\\ a_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ a_{n}^{\prime } & \vspace{6}\\ \end{array} $ ={T}^{ - 1 }\text{\hspace{1}} $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ ⇔ $3$\displaystyle{ $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ =T\text{\hspace{1}} $ \begin{array} a_{1}^{\prime } & \vspace{6}\\ a_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ a_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ --- (7)

の関係があることが分かる．

次に， $3$\displaystyle{{\displaystyle{R}}^{n}}$ から $3$\displaystyle{{\displaystyle{R}}^{n}}$ への線形写像 $3$\displaystyle{f:{\displaystyle{R}}^{n}\rightarrow {\displaystyle{R}}^{n}}$ を考え，この線形写像によって $3$\displaystyle{\displaystyle{b}=f$\displaystyle{a}$}$ と変換されるとする． $3$\displaystyle{f}$ の表現行列を $3$\displaystyle{A}$ とすると

$3$\displaystyle{ \displaystyle{b}= $ \begin{array} \hspace{1}{b}_{1} & \vspace{6}\\ \hspace{1}{b}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{b}_{n} & \vspace{6}\\ \end{array} $ }$ $3$\displaystyle{ =A\text{\hspace{1}} $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ --- (8)

であるが，これを (4) のように基底を明示して表記すると，

$3$\displaystyle{ \displaystyle{b}=\hspace{1}{b}_{1}\hspace{1}{\displaystyle{e}}_{1}+\hspace{1}{b}_{2}\hspace{1}{\displaystyle{e}}_{2}+\cdots +\hspace{1}{b}_{n}\hspace{1}{\displaystyle{e}}_{n} }$ $3$\displaystyle{ = $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ $ \begin{array} \hspace{1}{b}_{1} & \vspace{6}\\ \hspace{1}{b}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{b}_{n} & \vspace{6}\\ \end{array} $ }$ $3$\displaystyle{ = $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ \text{\hspace{1}}A\text{\hspace{1}} $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ --- (9)

となる．右辺において (5)，(7) を用いると

$3$\displaystyle{ $ \begin{array} \hspace{1}{\displaystyle{e}}_{1} & \hspace{1}{\displaystyle{e}}_{2} &\cdots & \hspace{1}{\displaystyle{e}}_{n} & \vspace{6}\\ \end{array} $ \text{\hspace{1}}A\text{\hspace{1}} $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ $3$\displaystyle{ = $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ \text{\hspace{1}}{T}^{ - 1 }AT\text{\hspace{1}} $ \begin{array} a_{1}^{\prime } & \vspace{6}\\ a_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ a_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ --- (10)

であり， $3$\displaystyle{\displaystyle{b}}$ を別の基底 $3$\displaystyle{ \{ \displaystyle{e}_{1}^{\prime },\text{\hspace{1}}\displaystyle{e}_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}\displaystyle{e}_{n}^{\prime } \} }$ で表記すると，

$3$\displaystyle{ \displaystyle{b}=b_{1}^{\prime }\displaystyle{e}_{1}^{\prime }+b_{2}^{\prime }\displaystyle{e}_{2}^{\prime }+\cdots +b_{n}^{\prime }\displaystyle{e}_{n}^{\prime } }$ $3$\displaystyle{ = $ \begin{array} \displaystyle{e}_{1}^{\prime } & \displaystyle{e}_{2}^{\prime } &\cdots & \displaystyle{e}_{n}^{\prime } & \vspace{6}\\ \end{array} $ $ \begin{array} b_{1}^{\prime } & \vspace{6}\\ b_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ b_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ --- (11)

であることから

$3$\displaystyle{ $ \begin{array} b_{1}^{\prime } & \vspace{6}\\ b_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ b_{n}^{\prime } & \vspace{6}\\ \end{array} $ ={T}^{ - 1 }AT\text{\hspace{1}} $ \begin{array} a_{1}^{\prime } & \vspace{6}\\ a_{2}^{\prime } & \vspace{6}\\ \vdots & \vspace{6}\\ a_{n}^{\prime } & \vspace{6}\\ \end{array} $ }$ --- (12)

の関係があることが分かる．

以上のことから，基底の変換

により，基底 $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ において $3$\displaystyle{ $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ と表されるベクトルは，別の基底 $3$\displaystyle{ \{ \displaystyle{e}_{1}^{\prime },\text{\hspace{1}}\displaystyle{e}_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}\displaystyle{e}_{n}^{\prime } \} }$ においては $3$\displaystyle{ {T}^{ - 1 }\text{\hspace{1}} $ \begin{array} \hspace{1}{a}_{1} & \vspace{6}\\ \hspace{1}{a}_{2} & \vspace{6}\\ \vdots & \vspace{6}\\ \hspace{1}{a}_{n} & \vspace{6}\\ \end{array} $ }$ で表され，基底 $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ における線形写像の表現行列 $3$\displaystyle{A}$ は，基底 $3$\displaystyle{ \{ \displaystyle{e}_{1}^{\prime },\text{\hspace{1}}\displaystyle{e}_{2}^{\prime },\text{\hspace{1}}\cdots ,\text{\hspace{1}}\displaystyle{e}_{n}^{\prime } \} }$ において $3$\displaystyle{{T}^{ - 1 }AT}$ と表されることがわかる．このことは，変換元の基底が基本ベクトル $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ でなくとも一般的に成り立つことである．

ホーム>>カテゴリー分類>>行列>>線形代数>>基底の変換

最終更新日： 2023年2月9日