基底と次元

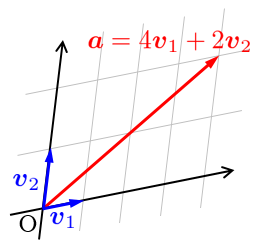
$基底の説明図$

ベクトル空間 $3$\displaystyle{V}$ の $3$\displaystyle{r}$ 個のベクトルの組 $3$\displaystyle{ \{ \hspace{1}{\displaystyle{v}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{r} \} }$ が1次独立(線形独立)で， $3$\displaystyle{V}$ の部分空間 $3$\displaystyle{W}$ を張るとき， $3$\displaystyle{ \{ \hspace{1}{\displaystyle{v}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{r} \} }$ を $3$\displaystyle{W}$ の基底，ベクトルの組の数 $3$\displaystyle{r}$ を $3$\displaystyle{W}$ の次元という．

$3$\displaystyle{W}$ の次元が $3$\displaystyle{r}$ （ $3$\displaystyle{r}$ 次元）であれば

$3$\displaystyle{dimW=r}$

と表す．

$3$\displaystyle{W}$ の任意のベクトル $3$\displaystyle{\displaystyle{a}}$ は基底 $3$\displaystyle{ \{ \hspace{1}{\displaystyle{v}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{r} \} }$ の1次結合として一意に表せ

$3$\displaystyle{ \displaystyle{a}=\hspace{1}{a}_{1}\hspace{1}{\displaystyle{v}}_{1}+\hspace{1}{a}_{2}\hspace{1}{\displaystyle{v}}_{2}+\cdots +\hspace{1}{a}_{r}\hspace{1}{\displaystyle{v}}_{r}\text{\hspace{1}}\in W }$ $3$\displaystyle{ $ \hspace{1}{a}_{1},\text{\hspace{1}}\hspace{1}{a}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{a}_{r}\in \displaystyle{R} $ }$

となる．

基底 $3$\displaystyle{ \{ \hspace{1}{\displaystyle{v}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{v}}_{r} \} }$ の個々のベクトルの大きさが 1 で，互いに直交する場合，つまり

$3$\displaystyle{ \| \hspace{1}{\displaystyle{v}}_{i} \| =1 }$
$3$\displaystyle{ \hspace{1}{\displaystyle{v}}_{i}\cdot \hspace{1}{\displaystyle{v}}_{j}=0 }$ $3$\displaystyle{ $i\neq j$ }$

のとき，この基底を正規直交基底という．

例えば， $3$\displaystyle{n}$ 次元実ベクトル空間 $3$\displaystyle{{\displaystyle{R}}^{n}}$ の基本ベクトル $3$\displaystyle{ \{ \hspace{1}{\displaystyle{e}}_{1},\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{2},\text{\hspace{1}}\cdots ,\text{\hspace{1}}\hspace{1}{\displaystyle{e}}_{n} \} }$ は1次独立であり， $3$\displaystyle{{\displaystyle{R}}^{n}}$ を張っているので， $3$\displaystyle{{\displaystyle{R}}^{n}}$ の基底となっている．さらに，個々のベクトルは大きさ 1 で互いに直交するので正規直交基底である．

■具体例

部分空間 $3$\displaystyle{ W=\left{{ \left.{ \left({ \begin{array}x& \vspace{6}\\ y& \vspace{6}\\ \end{array} }\right) }\right|x+2y=0 }\right}⊂{\displaystyle{R}}^{2} }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
の基底と次元を求める．

$3$\displaystyle{ x+2y=0 }$ より， $3$\displaystyle{x=- 2y}$

よって

$3$\displaystyle{\left({ \begin{array}x& \vspace{6}\\ y& \vspace{6}\\ \end{array} }\right)=\left({ \begin{array} - 2y & \vspace{6}\\ y& \vspace{6}\\ \end{array} }\right)=y\left({ \begin{array} - 2 & \vspace{6}\\ 1& \vspace{6}\\ \end{array} }\right)}$

となり，

$3$\displaystyle{W=\left({ \left({ \begin{array} - 2 & \vspace{6}\\ 1& \vspace{6}\\ \end{array} }\right) }\right)}$ 　（部分空間 $3$\displaystyle{W}$ は $3$\displaystyle{ \left({ \begin{array} - 2 & \vspace{6}\\ 1& \vspace{6}\\ \end{array} }\right) }$ で張られる部分空間である．）

また，

$3$\displaystyle{c\left({ \begin{array} - 2 & \vspace{6}\\ 1& \vspace{6}\\ \end{array} }\right)=\displaystyle{0}\Rightarrow \text{c=}0}$

より， $3$\displaystyle{ \left({ \begin{array} - 2 & \vspace{6}\\ 1& \vspace{6}\\ \end{array} }\right) }$ は1次独立である．

以上より，部分空間 $3$\displaystyle{W}$ の基底は $3$\displaystyle{\left{{ \left({ \begin{array} - 2 & \vspace{6}\\ 1& \vspace{6}\\ \end{array} }\right) }\right}}$ で，次元は $3$\displaystyle{dimW=1}$ である．

ホーム>>カテゴリー分類>>行列>>線形代数>>基底

最終更新日：2025年4月22日