グラフを平行移動した関数

関数 $3$\displaystyle{ y=f $x$ }$ のグラフを $3$x$ 軸方向に $3$a$ ， $3$y$ 軸方向に $3$b$ 平行移動（移動距離は軸の正の方向を正とする）したグラフを表す関数は

$3$\displaystyle{ y- b=f $ x- a $ }$ 　･･････(1)

となる．

ポイント： $3$x$ 軸方向に $3$a$ ， $3$y$ 軸方向に $3$b$ 平行移動した関数とは元の関数の $3$x$ を $3$\displaystyle{ x- a }$ に， $3$y$ を $3$\displaystyle{ y- b }$ に書き換えたものになる．

■式の導出

平行移動の考え方を具体的に説明する．

まず

$3$ y=x$ 　･･････(2)

の直線のグラフについて考える．

● $3$x$ 軸方向に平行移動したグラフを表す関数

例えば， $3$\displaystyle{ y=x }$ のグラフを $3$x$ 軸方向に4平行移動したグラフを表す関数を求める．

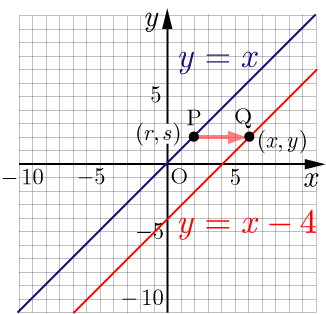
$3$\displaystyle{ y=x }$ 上の点 $3$\text{P}$ を $3$x$ 軸方向に4平行移動したものを点 $3$\text{Q}$ とし，点 $3$\text{P}$ ， $3$\text{Q}$ の座標をそれぞれ $3$\displaystyle{ $ r,s $ }$ ， $3$ $ x,y $$ とする．点 $3$\text{Q}$ の $3$x$ 座標の値は点 $3$\text{P}$ の $3$x$ 座標の値 $3$r$ に4を加えたものとなり，点 $3$\text{Q}$ の $3$y$ 座標の値は点 $3$\text{P}$ の $3$y$ 座標の値 $3$s$ のままである．すなわち

$3$\displaystyle{ \{\begin{array}{lll} x=r+ 4 & \vspace{6}\\ y=s & \vspace{6}\\ \end{array} \rightarrow }$ $3$\displaystyle{ $ x,y $ = $ r+ 4,s $ }$ 　･･････(3)

の関係がある．これは点 $3$\text{Q}$ を点 $3$\text{P}$ の座標の値を用いて表しているが，逆に点 $3$\text{P}$ の座標を，点 $3$\text{Q}$ の座標の値 $3$x$ ， $3$y$ を使って表すと

$3$\displaystyle{ \{\begin{array}{lll} r=x- 4 & \vspace{6}\\ s=y & \vspace{6}\\ \end{array} \rightarrow }$ $3$\displaystyle{ $ r,s $ = $ x- 4,y $ }$ 　･･････(4)

となる．点 $3$\text{P}$ は $3$\displaystyle{ y=x }$ 上の点であるので

$3$\displaystyle{ r=s }$ 　･･････(5)

の関係がある．(5)の $3$r$ と $3$s$ に(4)の $3$\displaystyle{ r=x- 4 }$ ， $3$\displaystyle{ s=y }$ の関係を代入すると

$3$\displaystyle{ y= $ x- 4 $ }$ 　･･････(6)

となる．(6)は $3$x$ と $3$y$ の関係を表している．すなわち，この(6)が(2)の $3$\displaystyle{ y=x }$ のグラフを $3$x$ 軸方向に4平行移動したグラフを表す関数である．

ポイント： $3$x$ 軸方向に4平行移動した関数とは元の関数の $3$x$ を $3$\displaystyle{ x- 4 }$ に書き換えたものになる．

● $3$y$ 軸方向に平行移動したグラフを表す関数

例えば， $3$\displaystyle{ y=x }$ のグラフを $3$y$ 軸方向に4平行移動したグラフを表す関数を求める．

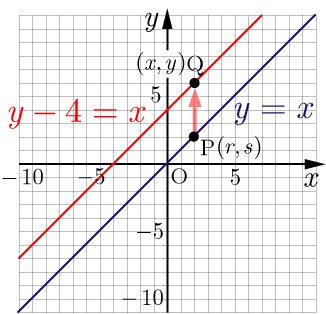
$3$\displaystyle{ y=x }$ 上の点 $3$\text{P}$ を $3$y$ 軸方向に4平行移動したものを点 $3$\text{Q}$ とし，点 $3$\text{P}$ ， $3$\text{Q}$ の座標をそれぞれ $3$\displaystyle{ $ r,s $ }$ ， $3$ $ x,y $$ とする．点 $3$\text{Q}$ の $3$x$ 座標の値は点 $3$\text{P}$ の $3$x$ 座標の値 $3$r$ のままであり，点 $3$\text{Q}$ の $3$y$ 座標の値は点 $3$\text{P}$ の $3$y$ 座標の値 $3$s$ に4を加えたものとなる．すなわち

$3$\displaystyle{ \{\begin{array}{lll}x=r& \vspace{6}\\ y=s+4& \vspace{6}\\ \end{array} \text{ }\rightarrow \text{ } $ x,y $ = $ r,s+4 $ }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
　･･････(7)

$3$\displaystyle{ \{\begin{array}{lll}r=x& \vspace{6}\\ s=y- 4& \vspace{6}\\ \end{array} \text{ }\rightarrow \text{ } $ r,s $ = $ x,y- 4 $ }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
　･･････(8)

となる．点 $3$\text{P}$ は $3$\displaystyle{ y=x }$ 上の点であるので

$3$\displaystyle{ r=s }$ 　･･････(5)

の関係がある．(5)の $3$r$ と $3$s$ に(8)の $3$\displaystyle{ r=x }$ ， $3$\displaystyle{ s=x- 4 }$ の関係を代入すると

$3$\displaystyle{ $ y- 4 $ =x }$ 　･･････(9)

となる．(9)は $3$x$ と $3$y$ の関係を表している．すなわち，この(9)が(2)の $3$\displaystyle{ y=x }$ のグラフを $3$y$ 軸方向に4平行移動したグラフを表す関数である．

ポイント： $3$y$ 軸方向に4平行移動した関数とは元の関数の $3$y$ を $3$\displaystyle{ y- 4 }$ に書き換えたものになる．

以上の基本的な考え方を基にして

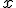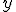● $3$x$ 軸方向と $3$y$ 軸方向の平行移動を組み合わせたグラフを表す関数

$3$\displaystyle{ y=f $x$ }$ のグラフを $3$x$ 軸方向に $3$a$ ， $3$y$ 軸方向に $3$b$ 平行移動したグラフを表す関数を求める．

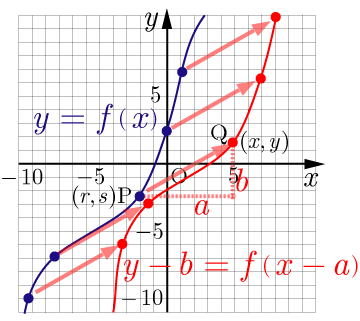
$3$\displaystyle{ y=f $x$ }$ 上の点 $3$\text{P}$ を $3$x$ 軸方向に $3$a$ ， $3$y$ 軸方向に $3$b$ 平行移動したものを点 $3$\text{Q}$ とし，点 $3$\text{P}$ ， $3$\text{Q}$ の座標をそれぞれ $3$\displaystyle{ $ r,s $ }$ ， $3$ $ x,y $$ とする．点 $3$\text{Q}$ の $3$x$ 座標の値は点 $3$\text{P}$ の $3$x$ 座標の値 $3$r$ に $3$a$ を加えたものとなり，点 $3$\text{Q}$ の $3$y$ 座標の値は点 $3$\text{P}$ の $3$y$ 座標の値 $3$s$ に $3$b$ を加えたものとなる．すなわち

$3$\displaystyle{ \{\begin{array}{lll}x=r+a& \vspace{6}\\ y=s+b& \vspace{6}\\ \end{array} \text{ }\rightarrow \text{ } $ x,y $ = $ r+a,s+b $ }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
　･･････(10)

$3$\displaystyle{ \{\begin{array}{lll}r=x- a& \vspace{6}\\ s=y- b& \vspace{6}\\ \end{array} \text{ }\rightarrow \text{ } $ r,s $ = $ x- a,y- b $ }$
TeXに変換設定していない数学記号や，特殊文字が含まれています。今後直していきます。
　･･････(11)