| ||||||||||||
|
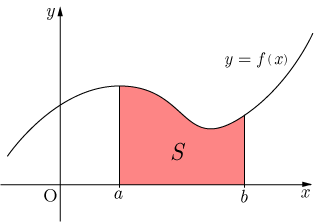
定積分と面積
定積分は,関数
の曲線と 軸で挟まれた領域で,区間
の面積を表す.ただし,区間
で
とする.
■解説
関数 の曲線と
軸で挟まれた領域で,区間
の面積を
とする.ただし,区間
で
,
とする.
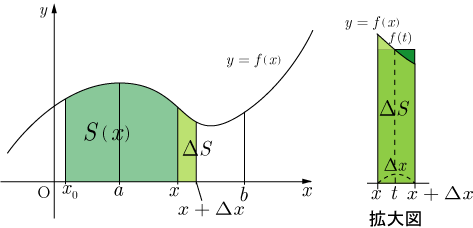
が
から
に増加したときの
の増加量を
とすると
と表すことができる.拡大図より , となる
が存在することがわかる.この関係は
の時も成り立つ.
のとき,
,
となることから
となり, は
不定積分であることが解る.
よって,定積分の定義より
と表される.すなわち,
は,関数
の曲線と
軸で挟まれた領域で,区間
の面積となる.
■参考
定積分を,微小面積を足し合わせたものであるという考え方がある.この考え方は物理現象等を理解するときに非常に大切である.以下に簡単に説明する.(和の極限としての定積分の定義を参照のこと)
まず,区間 を
等分して
個の長方形を考える.(下図の場合は
である.また単純化するために等分割している.)
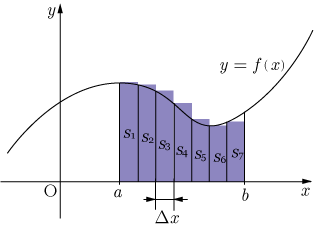
ただし
個の長方形の面積の総和を
とすると
となる.下図より,分割数を増やすと (ある区間の関数
と
軸で挟まれた面積)と
の差が小さくなっているのが解る.
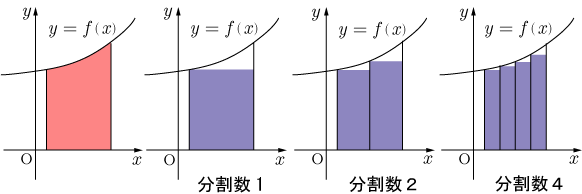
このことから, にすると
となる.これを式で表すと
ただし
となる.この面積 値が定積分 のことで
ただし
である.
参考:区分求積法
最終更新日: 2024年7月2日