2倍角の公式

$sin2\alpha =2sin\alpha cos\alpha$  ⇒公式の導出 

${\displaystyle cos2\alpha ={cos}^2\alpha -{sin}^2\alpha }$  ⇒公式の導出 

${\displaystyle \begin{array}{l}=2{cos}^2\alpha -1\\ =1-2{sin}^2\alpha \end{array}}$ 

${\displaystyle tan2\alpha =\frac{2tan\alpha }{1-{tan}^2\alpha }}$　 ⇒公式の導出 

　

■公式の導出

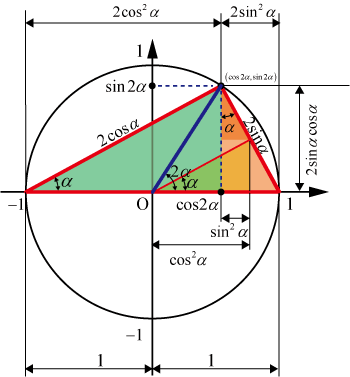これらの式は加法定理において，$\beta =\alpha$とすることにより求めることができる．

●sinの2倍角の公式の導出

${\displaystyle sin2\alpha =sin\left(\alpha +\alpha \right)}$ 

• ${\displaystyle =sin\alpha cos\alpha +cos\alpha sin\alpha }$
• 　　（加法定理を参照）

${\displaystyle =2sin\alpha cos\alpha }$ 

●cosの2倍角の公式の導出

${\displaystyle cos2\alpha =cos\left(\alpha +\alpha \right)}$ 

• ${\displaystyle =cos\alpha cos\alpha -sin\alpha sin\alpha }$
• 　　　（加法定理を参照）

${\displaystyle ={cos}^2\alpha -{sin}^2\alpha }$　　･･････(1) 

(1)に三角関数の相互関係 ${\displaystyle {sin}^2\alpha +{cos}^2\alpha =1}$ から得られる ${\displaystyle {sin}^2\alpha =1-{cos}^2\alpha }$ を代入すると，

${\displaystyle \begin{array}{l}={cos}^2\alpha -\left(1-{cos}^2\alpha \right)\\ =2{cos}^2\alpha -1\end{array}}$  

すなわち，

${\displaystyle cos2\alpha =2{cos}^2\alpha -1}$  

のcosの2倍角の公式が得られる．

同様にして，(1)に三角関数の相互関係 ${\displaystyle {sin}^2\alpha +{cos}^2\alpha =1}$ から得られる ${\displaystyle {cos}^2\alpha =1-{sin}^2\alpha }$  を代入すると，

$\begin{array}{l}=\left(1-{sin}^2\alpha \right)-{sin}^2\alpha \\ =1-2{sin}^2\alpha \end{array}$  

すなわち，

${\displaystyle cos2\alpha =1-2{sin}^2\alpha }$  

の別のcosの2倍角の公式が得られる．

●tanの2倍角の公式の導出

${\displaystyle tan2\alpha =tan\left(\alpha +\alpha \right)}$ 

${\displaystyle =\frac{tan\alpha +tan\alpha }{1-tan\alpha tan\alpha }}$　　（加法定理を参照）

${\displaystyle =\frac{2tan\alpha }{1-{tan}^2\alpha }}$ 

 

ホーム>>カテゴリー分類>>三角関数>>2倍角の公式

最終更新日： 2023年3月2日