媒介変数表示における導関数
,
と媒介変数で表すことのできる
の関数
がある.このときの,
は
となる.
■導出
を
に関して解いて
が得られたとする.すると,
と表すことができる.
ここで,
(
) である.
ここで,
とおくと,
となる.また,
ならば
となる. よって,
微分に関する基本式を参照
●グラフを用いた媒介変数表示における導関数の説明
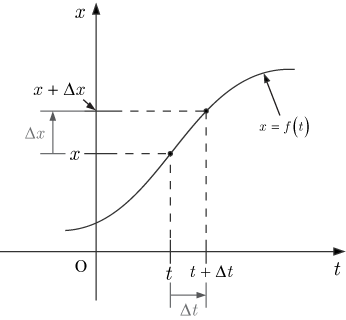
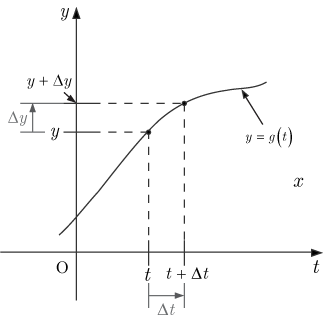
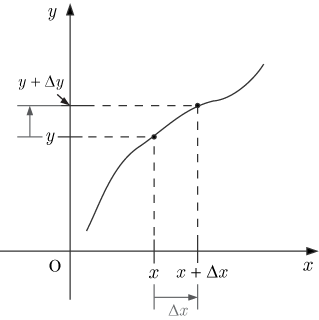
,
とする.
の分母,分子を
で割ると
のとき
となる.
よって
まとめると
となる.
ホーム>>カテゴリー分類>>微分>>媒介変数表示における導関数
最終更新日
2025年4月27日


