方向場 (direction field)

1階の微分方程式 ${\displaystyle y^{\prime }=f(x,y)}$ は，この微分方程式の解 ${\displaystyle y(x)}$ を表す曲線上の点 ${\displaystyle (x,y)}$ における勾配（接線の傾き）を表す．

${\displaystyle xy}$平面上の点 ${\displaystyle (x,y)}$ において，傾き ${\displaystyle f(x,y)}$ をもった短い線分（方向線素）を描き，平面上が方向線素で十分に覆われるように表したものを 方向場 (direction field) という．

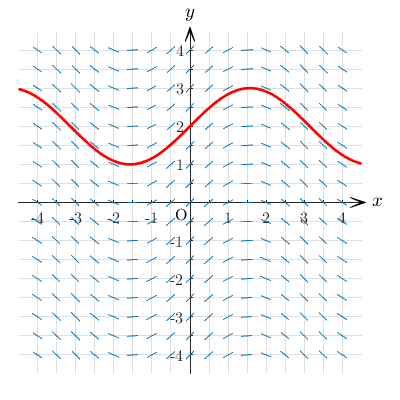
■例

${\displaystyle y^{\prime }=\cos x}$ の方向場

図において，方向場が多数の青い方向線素で示されており，初期条件 ${\displaystyle y(0)=2}$ を満たす特殊解 ${\displaystyle y=\sin x+2}$ が赤線で示されている．解の曲線は方向場に沿っていることがわかる．

方向場の利点

方向場を描くと，ある点 ${\displaystyle (x_0,y_0)}$ を通り，その方向場に沿った曲線をおおまかに描くことができ，その曲線は初期条件 ${\displaystyle y(x_0)=y_0}$ を満たす特殊解に対応している．つまり，実際に微分方程式を解かなくても，近似的にその解が表す曲線のグラフを描くことができるため，解の挙動を視覚的に把握することができる．

このことは，解析的に解くことができない複雑な微分方程式の解を近似的に得ることができるという面で実用的な方法であり，微分方程式の解を数値計算で求めるときの基本となる考えである．

ホーム>>カテゴリー分類>>微分>>微分方程式>>方向場

最終更新日：2023年6月9日