2変数関数のテイラー（Taylor）の定理の導出

$f (a + h, b + k) = f (a, b)$ $+ \frac{1}{1!} (h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}) f (a, b)$ $+ \frac{1}{2!} (h \frac{\partial}{\partial x} + {k \frac{\partial}{\partial y})}^{2} f (a, b)$ $+ \dots$ $+ \frac{1}{n!} (h \frac{\partial}{\partial x} {+ k \frac{\partial}{\partial y})}^{n} f (a, b)$ $+ R_{n + 1}$

$R_{n + 1}$ $= \frac{1}{(n + 1)!} (h \frac{\partial}{\partial x} {+ k \frac{\partial}{\partial y})}^{n + 1} f (a + θ h, b + θ k)$ 　　（ただし, $0 < θ < 1$ ）

■導出

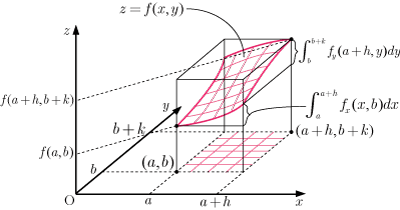
$f (a + h, b + k)$ は次のように表すことができる．

$f (a + h, b + k) = f (a, b)$ $+ \int_{a}^{a + h} f_{x} (x, b) d x$ $+ \int_{b}^{b + k} f_{y} (a + h, y) d y$

この式を部分積分すると　　　⇒積分はこちら

$= f (a, b) + h f_{x} (a, b) + \frac{1}{2} h^{2} f_{x x} (a, b)$ $+ \frac{1}{6} h^{3} f_{x x x} (a, b)$

$+ \dots + \frac{1}{(n - 1)!} h^{n - 1} {(\frac{\partial}{\partial x})}^{n - 1} f (a, b)$ $+ \frac{1}{n!} h^{n} {(\frac{\partial}{\partial x})}^{n} f (a, b)$

$+ \int_{a}^{a + h} {- \frac{1}{(n + 1)!} {(a + h - x)}^{n + 1}}^{'} {(\frac{\partial}{\partial x})}^{n + 1} f (x, b) d x$

$+ k f_{y} (a + h, b) + \frac{1}{2} k^{2} f_{y y} (a + h, b)$ $+ \frac{1}{6} k^{3} f_{y y y} (a + h, b)$

$+ \dots + \frac{1}{(n - 1)!} k^{n - 1} {(\frac{\partial}{\partial y})}^{n - 1} f (a + h, b)$ $+ \frac{1}{n!} k^{n} {(\frac{\partial}{\partial y})}^{n} f (a + h, b)$

$+ \int_{b}^{b + k} {- \frac{1}{(n + 1)!} {(b + k - y)}^{n + 1}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y$

となることがわかる．

次に $f_{y} (a + h, b)$ ， $f_{yy} (a + h, b)$ ， $f_{yyy} (a + h, b)$ ，･･･， ${(\frac{\partial}{\partial y})}^{n - 1} f (a + h, b)$ ， ${(\frac{\partial}{\partial y})}^{n} f (a + h, b)$ について考える．

$f_{y} (a + h, b)$ は次のように書き換えることができる．

$f_{y} (a + h, b) = f_{y} (a, b) + \int_{a}^{a + h} \frac{\partial}{\partial x} f_{y} (x, b) d x$

同様に

$f_{y y} (a + h, b) = f_{y y} (a, b) + \int_{a}^{a + h} \frac{\partial}{\partial x} f_{y y} (x, b) d x$

$f_{y y y} (a + h, b) = f_{y y y} (a, b) + \int_{a}^{a + h} \frac{\partial}{\partial x} f_{y y y} (x, b) d x$

・・・・・・

${(\frac{\partial}{\partial y})}^{n - 1} f (a + h, b) = {(\frac{\partial}{\partial y})}^{n - 1} f (a, b)$ $+ \int_{a}^{a + h} {(\frac{\partial}{\partial y})}^{n - 1} f (x, b) d x$

${(\frac{\partial}{\partial y})}^{n} f (a + h, b) = {(\frac{\partial}{\partial y})}^{n} f (a, b)$ $+ \int_{a}^{a + h} {(\frac{\partial}{\partial y})}^{n} f (x, b) d x$

となる．よって

$f (a + h, b + k)$

$= f (a, b) + h f_{x} (a, b) + \frac{1}{2} h^{2} f_{x x} (a, b)$ $+ \frac{1}{6} h^{3} f_{x x x} (a, b)$

$+ \dots + \frac{1}{(n - 1)!} h^{n - 1} {(\frac{\partial}{\partial x})}^{n - 1} f (a, b) \frac{1}{n!} h^{n} {(\frac{\partial}{\partial x})}^{n} f (a, b)$ $+ \int_{a}^{a + h} {- \frac{1}{(n + 1)!} {(a + h - x)}^{n + 1}}^{'} {(\frac{\partial}{\partial x})}^{n + 1} f (x, b) d x$

$+ k f_{y} (a, b) + \frac{1}{2} k^{2} f_{y y} (a, b) + \frac{1}{6} k^{3} f_{y y y} (a, b)$ $+ \dots$ $+ \frac{1}{(n - 1)!} k^{n - 1} {(\frac{\partial}{\partial y})}^{n - 1} f (a, b)$ $+ \frac{1}{n!} k^{n} {(\frac{\partial}{\partial y})}^{n} f (a, b)$

$+ k \int_{a}^{a + h} \frac{\partial}{\partial x} f_{y} (x, b) d x$ $+ \frac{1}{2} k^{2} \int_{a}^{a + h} \frac{\partial}{\partial x} f_{y y} (x, b) d x$ $+ \frac{1}{6} k^{3} \int_{a}^{a + h} \frac{\partial}{\partial x} f_{y y y} (x, b) d x$

$+ \dots$ $+ \frac{1}{(n - 1)!} k^{n - 1} \int_{a}^{a + h} {(\frac{\partial}{\partial y})}^{n - 1} f (x, b) d x$ $+ \frac{1}{n!} k^{n} \int_{a}^{a + h} {(\frac{\partial}{\partial y})}^{n} f (x, b) d x$

$+ \int_{b}^{b + k} {\{- \frac{1}{(n + 1)!} {(b + k - y)}^{n + 1}\}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y$

さらに部分積分をすると　　　⇒積分はこちら

$f (a + h, b + k)$

$= f (a, b) + h f_{x} (a, b) + \frac{1}{2} h^{2} f_{x x} (a, b)$ $+ \frac{1}{6} h^{3} f_{x x x} (a, b)$ $+ \dots + \frac{1}{(n - 1)!} h^{n - 1} {(\frac{\partial}{\partial x})}^{n - 1} f (a, b)$ $+ \frac{1}{n!} h^{n} {(\frac{\partial}{\partial x})}^{n} f (a, b)$

$+ \int_{a}^{a + h} {- \frac{1}{(n + 1)!} {(a + h - x)}^{n + 1}}^{'} {(\frac{\partial}{\partial x})}^{n + 1} f (x, b) d x$

$+ k [h f_{y x} (a, b) + \frac{1}{2} h^{2} f_{y x x} (a, b) + \dots$ $+ \frac{1}{(n - 1)!} h^{n - 1} {(\frac{\partial}{\partial x})}^{n - 1} \frac{\partial}{\partial y} f (a, b)$

$+ \int_{a}^{a + h} {- \frac{1}{n!} {(a + h - x)}^{n}}^{'} {(\frac{\partial}{\partial x})}^{n} \frac{\partial}{\partial y} f (x, b) d x]$

$+ \frac{1}{2} k^{2} [h f_{y y x} (a, b) + \frac{1}{2} h^{2} f_{y y x x} (a, b)$ $+ \dots$ $+ \frac{1}{(n - 2)!} h^{n - 2} {(\frac{\partial}{\partial x})}^{n - 2} {(\frac{\partial}{\partial y})}^{2} f (a, b)$

$+ \int_{a}^{a + h} {- \frac{1}{(n - 1)!} {(a + h - x)}^{n - 1}}^{'} {(\frac{\partial}{\partial x})}^{n - 1} {(\frac{\partial}{\partial y})}^{2} f (x, b) d x]$

$+ \frac{1}{6} k^{3} [h f_{y y y x} (a, b) + \frac{1}{2} h^{2} f_{y y y x x} (a, b)$ $+ \dots$ $\begin{array}{l} + \frac{1}{(n - 3)!} h^{n - 3} {(\frac{\partial}{\partial x})}^{n - 3} {(\frac{\partial}{\partial y})}^{3} f (a, b) \end{array}$

$+ \int_{a}^{a + h} {- \frac{1}{(n - 2)!} {(a + h - x)}^{n - 2}}^{'} {(\frac{\partial}{\partial x})}^{n - 2} {(\frac{\partial}{\partial y})}^{3} f (x, b) d x]$

$+ \cdot \cdot \cdot \cdot \cdot \cdot +$

$+ \frac{1}{(n - 1)!} k^{n - 1} [h \frac{\partial}{\partial x} {(\frac{\partial}{\partial y})}^{n - 1} f (a, b)$ $+ \int_{a}^{a + h} {- \frac{1}{2!} {(a + h - x)}^{2}}^{'} {(\frac{\partial}{\partial x})}^{2} {(\frac{\partial}{\partial y})}^{n - 1} f (x, b) d x]$

$+ \frac{1}{n!} k^{n} + \int_{a}^{a + h} {\{- (a + h - x)\}}^{'} (\frac{\partial}{\partial x}) {(\frac{\partial}{\partial y})}^{n} f (x, b) d x$

$+ \int_{b}^{b + k} {- \frac{1}{(n + 1)!} {(b + k - y)}^{n + 1}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y$

この式を整理すると

$= f (a, b) + h f_{x} (a, b) + k f_{y} (a, b)$ $+ \frac{1}{2} h^{2} f_{x x} (a, b)$ $+ h k f_{y x} (a, b) + \frac{1}{2} k^{2} f_{y y} (a, b)$

$+ \frac{1}{6} h^{3} f_{x x x} (a, b) + \frac{1}{2} h^{2} k f_{y x x} (a, b)$ $+ \frac{1}{2} h k^{2} f_{y y x} (a, b)$ $+ \frac{1}{6} k^{3} f_{y y y} (a, b) + \dots$

$+ \frac{1}{n!} h^{n} {(\frac{\partial}{\partial x})}^{n} f (a, b)$ $+ \frac{1}{(n - 1)!} h^{n - 1} k {(\frac{\partial}{\partial x})}^{n - 1} \frac{\partial}{\partial y} f (a, b)$ $+ \frac{1}{2 (n - 2)!} h^{n - 2} k^{2} {(\frac{\partial}{\partial x})}^{n - 2} {(\frac{\partial}{\partial y})}^{2} f (a, b)$

$+ \frac{1}{6 (n - 3)!} h^{n - 3} k^{3} {(\frac{\partial}{\partial x})}^{n - 3} {(\frac{\partial}{\partial y})}^{3} f (a, b)$ $+ \dots$ $+ \frac{1}{(n - 1)!} h k^{n - 1} \frac{\partial}{\partial x} {(\frac{\partial}{\partial y})}^{n - 1}$ $+ f (a, b)$ $+ \frac{1}{n!} k^{n} {(\frac{\partial}{\partial y})}^{n} f (a, b)$

$+ \int_{a}^{a + h} {- \frac{1}{(n + 1)!} {(a + h - x)}^{n + 1}}^{'} {(\frac{\partial}{\partial x})}^{n + 1} f (x, b) d x$

$+ k \int_{a}^{a + h} {- \frac{1}{n!} {(a + h - x)}^{n}}^{'} {(\frac{\partial}{\partial x})}^{n} \frac{\partial}{\partial y} f (x, b) d x$

$+ \frac{1}{2} k^{2} \int_{a}^{a + h} {- \frac{1}{(n - 1)!} {(a + h - x)}^{n - 1}}^{'} {(\frac{\partial}{\partial x})}^{n - 1} {(\frac{\partial}{\partial y})}^{2} f (x, b) d x$

$+ \frac{1}{6} k^{3} \int_{a}^{a + h} {- \frac{1}{(n - 2)!} {(a + h - x)}^{n - 2}}^{'} {(\frac{\partial}{\partial x})}^{n - 2} {(\frac{\partial}{\partial y})}^{3} f (x, b) d x + \dots$

$+ \frac{1}{(n - 1)!} k^{n - 1} \int_{a}^{a + h} {- \frac{1}{2!} {(a + h - x)}^{2}}^{'} {(\frac{\partial}{\partial x})}^{2} {(\frac{\partial}{\partial y})}^{n - 1} f (x, b) d x$

$+ \frac{1}{n!} k^{n} \int_{a}^{a + h} {- {(a + h - x)}^{2}}^{'} {\frac{\partial}{\partial x} (\frac{\partial}{\partial y})}^{n} f (x, b) d x$

$+ \int_{b}^{b + k} \frac{1}{(n + 1)!} {- {(b + k - y)}^{n + 1}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y$

$= f (a, b) + \frac{1}{1!} {h f_{x} (a, b) + k f_{y} (a, b)}$ $+ \frac{1}{2!} {h^{2} f_{x x} (a, b)$ $+ 2 h k f_{y x} (a, b) + k^{2} f_{y y} (a, b)}$

$+ \frac{1}{3!} {h^{3} f_{x x x} (a, b) + 3 h^{2} k f_{y x x} (a, b)$ $+ 3 h k^{2} f_{y y x} (a, b)$ $+ k^{3} f_{y y y} (a, b)} + \dots$

$+ \frac{1}{n!} {{(h \frac{\partial}{\partial x})}^{n} f (a, b) + n {(h \frac{\partial}{\partial x})}^{n - 1} k \frac{\partial}{\partial y} f (a, b)$ $+ \frac{n (n - 1)}{2!} {(h \frac{\partial}{\partial x})}^{n - 2} {(k \frac{\partial}{\partial y})}^{2} f (a, b)$

$+ \frac{n (n - 1) (n - 2)}{3!} {(h \frac{\partial}{\partial x})}^{n - 3} {(k \frac{\partial}{\partial y})}^{3} f (a, b)$ $+ \dots + {(k \frac{\partial}{\partial y})}^{n} f (a, b)}$

$+ \frac{1}{(n + 1)!} [\int_{a}^{a + h} {- {(a + h - x)}^{n + 1}}^{'} {(\frac{\partial}{\partial x})}^{n + 1} f (x, b) d x$

$+ (n + 1) k \int_{a}^{a + h} {- {(a + h - x)}^{n}}^{'} {(\frac{\partial}{\partial x})}^{n} \frac{\partial}{\partial y} f (x, b) d x$

$+ \frac{(n + 1) n}{2} k^{2} \int_{a}^{a + h} {- {(a + h - x)}^{n - 1}}^{'} {(\frac{\partial}{\partial x})}^{n - 1} {(\frac{\partial}{\partial y})}^{2} f (x, b) d x$

$+ \frac{(n + 1) n (n - 1)}{3!} k^{3} \int_{a}^{a + h} {- {(a + h - x)}^{n - 2}}^{'} {(\frac{\partial}{\partial x})}^{n - 2} {(\frac{\partial}{\partial y})}^{3} f (x, b) d x + \dots$

$+ \frac{(n + 1) n (n - 1) \dots 4 \cdot 3}{(n - 1)!} k^{n - 1} \int_{a}^{a + h} {- {(a + h - x)}^{2}}^{'} {(\frac{\partial}{\partial x})}^{2} {(\frac{\partial}{\partial y})}^{n - 1} f (x, b) d x$

$+ \frac{(n + 1) n (n - 1) \dots 3 \cdot 2}{n!} k^{n} \int_{a}^{a + h} {- (a + h - x)}^{'} {\frac{\partial}{\partial x} (\frac{\partial}{\partial y})}^{n} f (x, b) d x]$

$+ \int_{b}^{b + k} \frac{1}{(n + 1)!} {- {(b + k - y)}^{n + 1}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y$

$= f (a, b) + \frac{1}{1!} (h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}) f (a, b)$ $+ \frac{1}{2!} (h \frac{\partial}{\partial x}$ ${+ k \frac{\partial}{\partial y})}^{2} f (a, b)$

$+ \frac{1}{3!} {(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y})}^{3} f (a, b)$ $+ \dots$ $+ \frac{1}{n!} {(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y})}^{n} f (a, b)$

$+ \frac{1}{(n + 1)!} [\{\sum_{r = 0}^{n}_{n + 1} C_{r} k^{r} \int_{a}^{a + h} {- {(a + h - x)}^{n - r + 1}}^{'} {(\frac{\partial}{\partial x})}^{n - r + 1} {(\frac{\partial}{\partial y})}^{r} f (x, b) d x\}$

$+ \int_{b}^{b + k} {- {(b + k - y)}^{n + 1}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y]$

ここで，

$\frac{1}{(n + 1)!} [\{\sum_{r = 0}^{n}_{n + 1} C_{r} k^{r} \int_{a}^{a + h} {- {(a + h - x)}^{n - r + 1}}^{'} {(\frac{\partial}{\partial x})}^{n - r + 1} {(\frac{\partial}{\partial y})}^{r} f (x, b) d x\}$

$+ \int_{b}^{b + k} {- {(b + k - y)}^{n + 1}}^{'} {(\frac{\partial}{\partial y})}^{n + 1} f (a + h, y) d y]$

を $R_{n + 1}$ に置き換えると

$= f (a, b)$ $+ \frac{1}{1!} (h \frac{\partial}{\partial x}$ $+ k \frac{\partial}{\partial y}) f (a, b)$ $+ \frac{1}{2!} (h \frac{\partial}{\partial x}$ ${+ k \frac{\partial}{\partial y})}^{2} f (a, b)$ $+ \frac{1}{3!} (h \frac{\partial}{\partial x}$ ${+ k \frac{\partial}{\partial y})}^{3} f (a, b)$ $+ \dots$ $+ \frac{1}{n!} (h \frac{\partial}{\partial x}$ ${+ k \frac{\partial}{\partial y})}^{n} f (a, b)$ $+ R_{n + 1}$

となる．しかし $R_{n + 1}$

$R_{n + 1} = \frac{1}{(n + 1)!} {(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y})}^{n + 1} f (a + θ h, b + θ k)$

である．

ホーム>>カテゴリー別分類>>微分>>偏微分>>2変数のテイラーの定理>>2変数関数のテイラーの定理の導出

学生スタッフ作成
最終更新日： 2023年10月16日