微分 tanx
■導出
( 三角関数の相互関係より )
( 分数関数の微分 IIより)
( 基本となる関数の導関数より)
( 三角関数の相互関係より)
●幾何学的理解
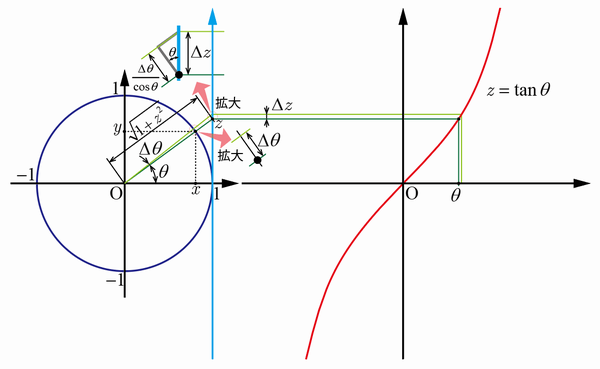
単位円と のグラフとの関係から の導関数を求める.
ホーム>>カテゴリー分類>>微分>>基本となる関数の導関数>>微分 tanx
最終更新日: 2024年7月12日
■導出
( 三角関数の相互関係より )
( 分数関数の微分 IIより)
( 基本となる関数の導関数より)
( 三角関数の相互関係より)

単位円と のグラフとの関係から の導関数を求める.
ホーム>>カテゴリー分類>>微分>>基本となる関数の導関数>>微分 tanx
最終更新日: 2024年7月12日