三角関数（三角比）の相互関係

■関係式

1. ${sin}^2\theta +{cos}^2\theta =1$  ⇒証明

2. ${\displaystyle tan\theta =\frac{sin\theta }{cos\theta }}$   （ただし，$cos\theta \ne 0$）  ⇒証明

3. ${\displaystyle {tan}^2\theta +1=\frac{1}{{cos}^2\theta }}$  （ただし， $cos\theta \ne 0$）  ⇒証明

　ここも参考にするとよい．

■証明

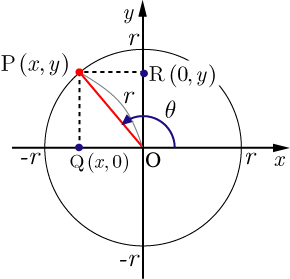1．三角関数の定義より（右図参照）

${\displaystyle sin\theta =\frac{y}{r}}$ ，${\displaystyle cos\theta =\frac{x}{r}}$より

• ${\displaystyle y=rsin\theta }$  ･･････(1)，

• ${\displaystyle x=rcos\theta }$ ･･････(2)

となる．△OQPにおいて，三平方の定理より

${\displaystyle \begin{array}{l}{\text{OQ}}^2+{\text{PQ}}^2={\text{OP}}^2\\ {\left|x\right|}^2+{\left|y\right|}^2=r^2\\ x^2+y^2=r^2\text{ ･･････(3)}\end{array}}$  

(3)に(1)，(2)を代入すると

${\displaystyle {\left(r\cos \theta \right)}^2+{\left(r\sin \theta \right)}^2=r^2}$

${sin}^2\theta +{cos}^2\theta =1$

が得られる．

2．三角関数の定義より

${\displaystyle sin\theta =\frac{y}{r}}$，${\displaystyle cos\theta =\frac{x}{r}}$，${\displaystyle tan\theta =\frac{y}{x}}$ 

よって

${\displaystyle tan\theta =\frac{y}{x}=\frac{\frac{y}{r}}{\frac{x}{r}}=\frac{sin\theta }{cos\theta }}$  

3．${\displaystyle {sin}^2\theta +{cos}^2\theta =1}$ の両辺を${\displaystyle {cos}^2\theta }$  で割ると

${\displaystyle \frac{{sin}^2\theta }{{cos}^2\theta }+\frac{{cos}^2\theta }{{cos}^2\theta }=\frac{1}{{cos}^2\theta }}$  

となる．${\displaystyle \frac{sin\theta }{cos\theta }=tan\theta }$  を上式に代入すると

${\displaystyle {tan}^2\theta +1=\frac{1}{{cos}^2\theta }}$  

の関係式が得られる．

 

 

ホーム>>カテゴリー分類>>三角関数>>三角関数の相互関係

最終更新日： 2023年3月9日