1・サイン・コサイン三角形を用いた三角関数の相互関係の導出

■三角比の相互関係

${\displaystyle {sin}^2\theta +{cos}^2\theta =1}$  ⇒こちらへ

${\displaystyle tan\theta =\frac{sin\theta }{cos\theta }}$  ⇒こちらへ

${\displaystyle {tan}^2\theta +1=\frac{1}{{cos}^2\theta }}$  ⇒こちらへ

■相互関係の導出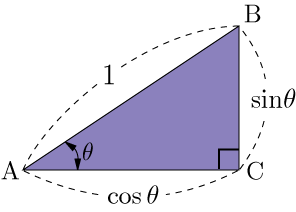

● ${\displaystyle {sin}^2\theta +{cos}^2\theta =1}$の導出

1・サイン・コサイン三角形の三平方の定理より，

${\displaystyle {\text{AB}}^2+{\text{AC}}^2={\text{AB}}^2}$  

の関係がある．各辺の長さは，

${\displaystyle \text{AB}=1}$  ${\displaystyle \text{BC}=\text{sin}\theta }$  ，${\displaystyle \text{AC}=\text{cos}\theta }$

である．よって，三角関数の相互関係の式の1つ，

${\displaystyle {sin}^2\theta +{cos}^2\theta =1}$  

が得られる．

●${\displaystyle tan\theta =\frac{sin\theta }{cos\theta }}$の導出

${\displaystyle tan\theta }$  の定義より，

${\displaystyle tan\theta =\frac{\text{BC}}{\text{AC}}=\frac{sin\theta }{cos\theta }}$  

となり，三角関数の相互関係の1つが得られる．

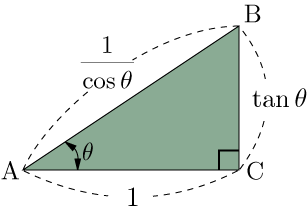
●${\displaystyle {tan}^2\theta +1=\frac{1}{{cos}^2\theta }}$の導出

さらに，各辺を，${\displaystyle \frac{1}{cos\theta }}$  倍すると，

${\displaystyle \text{AB}=\frac{1}{cos\theta }}$ ，${\displaystyle \text{BC}=sin\theta ·\frac{1}{cos\theta }=tan\theta }$ ，${\displaystyle \text{AC}=cos\theta ·\frac{1}{cos\theta }=1}$  

となる．三平方の定理より，

${\displaystyle {\left(tan\theta \right)}^2+1={\left(\frac{1}{cos\theta }\right)}^2}$ ⇒ ${\displaystyle {tan}^2\theta +1=\frac{1}{{cos}^2\theta }}$

となり三角関数の相互関係の式の1つが得られる．

 

 

ホーム>>カテゴリー分類>>三角関数>>1・サイン・コサイン三角形を用いた三角関数の相互関係の導出

最終更新日： 2023年3月2日