円の方程式(複素平面)

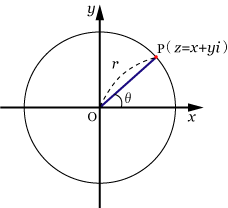● 複素平面上において，原点Oを中心とする半径  r  の 円の方程式

　複素数を ${\displaystyle z=x+yi}$   とすると

${\displaystyle \left|z\right|=r}$   （ ${\displaystyle r=\sqrt{x^2+y^2}}$ ）

極形式で表すと

${\displaystyle z=r\left(cos\theta +isin\theta \right)}$

となる．

　

● 複素平面上において，点C（ ${\displaystyle \alpha =a+bi}$  ）を中心とする半径  r   の 円の方程式

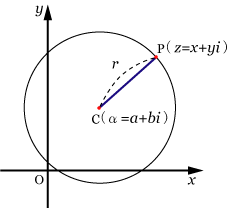複素数を ${\displaystyle z=x+yi}$   とすると

${\displaystyle \left|z-\alpha \right|=r}$

${\displaystyle \left|\left(x-yi\right)-\left(a+bi\right)\right|=r}$

${\displaystyle \left|\left(x-a\right)+\left(y-b\right)i\right|=r}$

ただし， ${\displaystyle \left(r=\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}\right)}$

となる．

● 複素平面において，点A（ ${\displaystyle \alpha =a+bi}$ ）と点B（ ${\displaystyle \beta =c+di}$ ）があり，線分ABを直径とする円の方程式

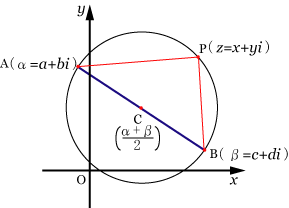　複素数を ${\displaystyle z=x+yi}$   とすると

${\displaystyle arg\frac{z-\alpha }{z-\beta }=\pm 90°}$

（円周角の定理と複素数平面での2直線のなす角を参照）

あるいは

円の中心が ${\displaystyle \frac{\alpha +\beta }{2}}$ ，円の半径が ${\displaystyle \frac{\left|\alpha -\beta \right|}{2}}$ となるので

${\displaystyle \left|z-\frac{\alpha +\beta }{2}\right|=\frac{\left|\alpha -\beta \right|}{2}}$

と表すこともできる．

　

【参考】円の方程式

 

ホーム>>カテゴリー分類>>幾何>>円の方程式

最終更新日 ： 2025年11月25日