定積分で定義された関数の微分
ポイント:
の部分には
を含んでいてはいけない. 積分範囲に注意.
は上端でなければならない.
■導出
●その1
関数
の原始関数を
とすると
となる.よって
●その2
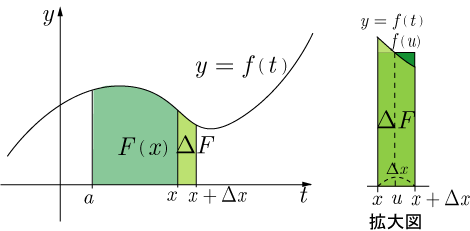 とおく.
が
から
に増加したときの
の増加量を
とすると,
とおく.
が
から
に増加したときの
の増加量を
とすると,
と表すことができる.
拡大図より ,
となる
が存在することがわかる.この関係は
の時も成り立つ.
のとき,
,
となることから
となる.よって
が得られる.
ホーム>>カテゴリー分類>>積分 >>定積分の基本式>>定積分で定義された関数の微分
最終更新日:
2025年9月5日
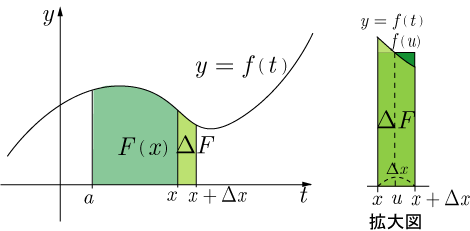 とおく.
が
から
に増加したときの
の増加量を
とすると,
とおく.
が
から
に増加したときの
の増加量を
とすると,