内積の値の幾何学的検討

■ ${\displaystyle 0°<\theta <90°}$ の場合

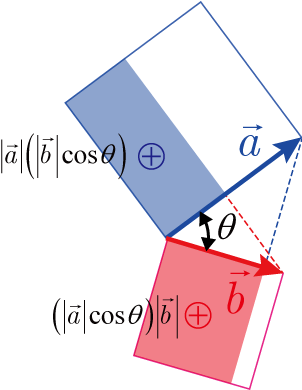
${\displaystyle 0°<\theta <90°}$ の場合

2つのベクトル( $\overrightarrow{a}$ ， $\overrightarrow{b}$ ) の内積の値は正になる．

${\displaystyle \overrightarrow{a}·\overrightarrow{b}>0}$

図の青線正方形は，${\displaystyle \overrightarrow{a}}$ を1辺とする正方形で，赤線正方形は，${\displaystyle \overrightarrow{b}}$ を1辺とする正方形である．

• 青色で塗られた長方形の面積の大きさは

  ${\displaystyle \overrightarrow{a}·\overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|cos\theta }$${\displaystyle =\left|\overrightarrow{a}\right|\left(\left|\overrightarrow{b}\right|\cos \theta \right)}$

  と解釈した場合の内積の値になる．

• 赤色で塗られた長方形の面積の大きさは

  ${\displaystyle \overrightarrow{a}·\overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|cos\theta }$${\displaystyle =\left(\left|\overrightarrow{a}\right|\cos \theta \right)\left|\overrightarrow{b}\right|}$

  と解釈した場合の内積の値になる．

■ ${\displaystyle 90°<\theta <180°}$の場合

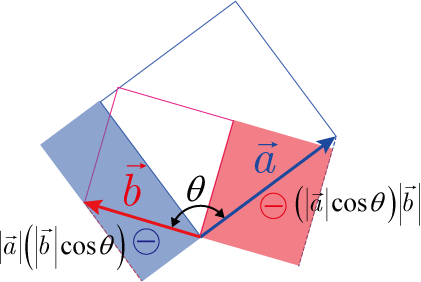
${\displaystyle 90°<\theta <180°}$の場合

2つのベクトル($\overrightarrow{a}$，$\overrightarrow{b}$) の内積の値は負になる．

${\displaystyle \overrightarrow{a}·\overrightarrow{b}<0}$

図の青線正方形は，${\displaystyle \overrightarrow{a}}$ を1辺とする正方形で，赤線正方形は，${\displaystyle \overrightarrow{b}}$ を1辺とする正方形である．

• 青色で塗られた長方形の面積の大きさは

  ${\displaystyle \overrightarrow{a}·\overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|cos\theta }$${\displaystyle =\left|\overrightarrow{a}\right|\left(\left|\overrightarrow{b}\right|\cos \theta \right)}$

  と解釈した場合の内積の値の絶対値になる．

• 赤色で塗られた長方形の面積の大きさは

  ${\displaystyle \overrightarrow{a}·\overrightarrow{b}=\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|cos\theta }$${\displaystyle =\left(\left|\overrightarrow{a}\right|\cos \theta \right)\left|\overrightarrow{b}\right|}$

  と解釈した場合の内積の値の絶対値になる．