内積
■内積の定義
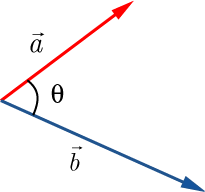 , のなす角を
とするとき
, のなす角を
とするとき
・・・・・・(1)
を , の内積という.
代わりに で表すこともある.
(1)より
, ・・・・・・(2)
アークコサイン(コサインの逆関数)を用いると
・・・・・・(3)
(3)が得られ, , のなす角を
を求めることができる.
■内積の成分表示
内積をベクトルの成分を用いて表す.
, とすると
となる⇒導出 .
, とすると
となる⇒導出 .
■内積の特徴
特に, , のなす角が90°のとき
(平面ベクトルの場合:,空間ベクトルの場合: )
となる.なぜならば,内積の定義より
が得られる.⇒ ベクトルの直交条件
ホーム>>カテゴリー分類>>ベクトル>>内積
最終更新日
2024年11月22日
 , のなす角を
とするとき
, のなす角を
とするとき