ベクトルの相等

お互いのベクトルの大きさと向きが等しいときベクトルは等しいと考えベクトルの相等という．

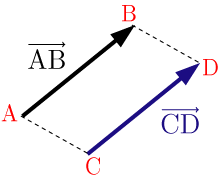
例えば，右図のように， ${\displaystyle \stackrel{⟶}{\text{AB}}}$ ， ${\displaystyle \stackrel{⟶}{\text{CD}}}$ があり，点 $\text{A}$ ，点 $\text{B}$ ，点 $\text{D}$ ，点 $\text{C}$ ，点 $\text{A}$ を結んでできる図形が平行四辺形であるなら， ${\displaystyle \stackrel{⟶}{\text{AB}}}$ と ${\displaystyle \stackrel{⟶}{\text{CD}}}$ の大きさと向きは等しい．よって， ${\displaystyle \stackrel{⟶}{\text{AB}}}$ と ${\displaystyle \stackrel{⟶}{\text{CD}}}$ は同じベクトルとなるので

${\displaystyle \stackrel{⟶}{\text{AB}}=\stackrel{⟶}{\text{CD}}}$  

と表す．

すなわち，ベクトルの相等とは，一方のベクトルを平行移動して他方のベクトルにちょうど重ね合わせることができるときのことをいう．

■成分表示を用いたベクトルの相当

${\displaystyle \overrightarrow{a}=\left(a_x,a_y\right)}$ ， ${\displaystyle \overrightarrow{b}=\left(b_x,b_y\right)}$

とすると

${\displaystyle \overrightarrow{a}=\overrightarrow{b}\iff }$   ${\displaystyle a_x=b_x}$ かつ  ${\displaystyle a_y=b_y}$

（2つのベクトルが等しければ，2つのベクトルの対応する成分同士はすべて等しい．また逆に，2つのベクトルの対応する成分同士がすべて等しければ，2つのベクトルは等しい．）

が成り立つ．

 

ホーム>>カテゴリー分類>>ベクトル>>ベクトルの相等

最終更新日 2025年9月27日