概念問題 解答

線形代数　二次曲線

問題3の解答

関数 ${\displaystyle y=\frac{1}{x}}$ のグラフは下の図のようになる．

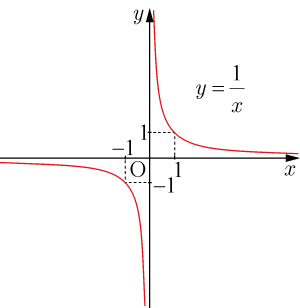
$x$ 軸と $y$ 軸が漸近線になっている．1，2，3，4の中から漸近線を持つグラフは4の双曲線だけである．よって，4か5であるが，グラフの形状は双曲線の特徴とよく似ている．

双曲線であるかどうかを検証する．

関数 ${\displaystyle y=\frac{1}{x}}$ のグラフを原点を中心に45°反時計回りに回転したグラフの関数を求める． $y=\frac{1}{x}$ のグラフ上の点 $\left(\begin{array}{c}x\\ y\end{array}\right)$ が原点を中心として反時計回りに45° $\left(\begin{array}{c}u\\ v\end{array}\right)$ とする．回転行列を用いて $\left(\begin{array}{c}x\\ y\end{array}\right)$ と $\left(\begin{array}{c}u\\ v\end{array}\right)$ の関係を式で表すと

$\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{cc}\cos 45°& -\sin 45°\\ \sin 45°& \cos 45°\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$ ${\displaystyle =\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{c}x\\ \frac{1}{x}\end{array}\right)}$ ${\displaystyle =\left(\begin{array}{c}\frac{x}{\sqrt{2}}-\frac{1}{\sqrt{2}x}\\ \frac{x}{\sqrt{2}}+\frac{1}{\sqrt{2}x}\end{array}\right)}$

となる．よって

${\displaystyle u=\frac{x}{\sqrt{2}}-\frac{1}{\sqrt{2}x}=\frac{1}{\sqrt{2}}\left(x-\frac{1}{x}\right)}$ ･････（1)

${\displaystyle v=\frac{x}{\sqrt{2}}+\frac{1}{\sqrt{2}x}=\frac{1}{\sqrt{2}}\left(x+\frac{1}{x}\right)}$ ･････(2)

(1)より

${\displaystyle u^2={\left\{\frac{1}{\sqrt{2}}\left(x-\frac{1}{x}\right)\right\}}^2}$ ${\displaystyle =\frac{1}{2}\left(x^2-2+\frac{1}{x^2}\right)}$ ${\displaystyle =-1+\frac{1}{2}\left(x^2+\frac{1}{x^2}\right)}$ ･････(3)

${\displaystyle v^2={\left\{\frac{1}{\sqrt{2}}\left(x+\frac{1}{x}\right)\right\}}^2}$ ${\displaystyle =\frac{1}{2}\left(x^2+2+\frac{1}{x^2}\right)}$ ${\displaystyle =1+\frac{1}{2}\left(x^2+\frac{1}{x^2}\right)}$ ･････(4)

(3)-(4)より

${\displaystyle u^2-v^2=-2}$

${\displaystyle \frac{u^2}{2}-\frac{v^2}{2}=-1}$

となり，双曲線の方程式となっている．よって反比例のグラフ ${\displaystyle y=\frac{1}{x}}$ は双曲線である.

よって，正解は3である．