たわみ曲線の微分方程式
ヤング率が
で表される関係が成り立つ.この関係式のことをたわみ曲線の微分方程式という.
■導出
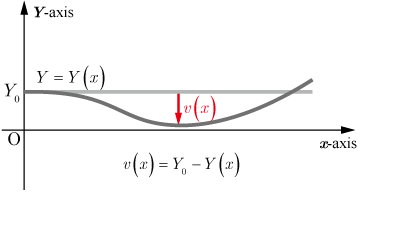 荷重によって梁がたわむ場合,下方にたわむことが多い.そのため,たわみ量
荷重によって梁がたわむ場合,下方にたわむことが多い.そのため,たわみ量
となる関係が成り立つ.
一方,ヤング率が
という関係がある.⇒ここを参照
(1)を(2)に代入すると
となる.
最終更新日2025年4月22日
ヤング率が
で表される関係が成り立つ.この関係式のことをたわみ曲線の微分方程式という.
 荷重によって梁がたわむ場合,下方にたわむことが多い.そのため,たわみ量
荷重によって梁がたわむ場合,下方にたわむことが多い.そのため,たわみ量
となる関係が成り立つ.
一方,ヤング率が
という関係がある.⇒ここを参照
(1)を(2)に代入すると
となる.
最終更新日2025年4月22日