加法定理の証明
単位円上に点
P,Q
がある。
OP
と
x
軸のなす角を
α
,
OQ
と
x
軸のなす角を
β
とする。(下図)
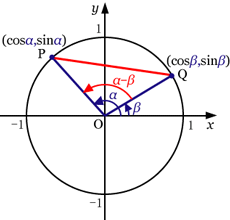
三角形
OPQ
を考え,余弦定理より,
PQ
2
=
OP
2
+
OQ
2
−
2OP⋅OQcos(
α−β
)
=
1
2
+
1
2
−2⋅1⋅1⋅cos(
α−β
)
=2−2cos(
α−β
)
・・・(1)
線分
PQ
の長さを点
P
,点
Q
の座標成分を用いて表すと,
PQ
2
=
(
cosβ−cosα
)
2
+
(
sinβ−sinα
)
2
=
cos
2
β−2+
cos
2
α+
sin
2
β−2+
sin
2
α
|
=2−2(
sinαsinβ+
cosαcosβ
)
| ・・・(2) |
(1),(2)より,
2−2cos(
α−β
)=
2−2(
cosαcosβ+sinαsinβ
)
よって,
cos(
α−β
)=
cosαcosβ+sinαsinβ
・・・(3)
(3)を用いて他の加法定理の公式を導くことができる。
|
cos(
α+β
)
| ⇒ |
|
|
sin(
α+β
)
| ⇒ |
|
|
sin(
α-β
)
| ⇒ |
|
|
tan(
α+β
)
| ⇒ |
|
|
tan(
α-β
)
| ⇒ |
戻る
[
か]
[
か行]
[
索引トップ]

