減衰振動：不足減衰 (under damping)

x 軸上を単振動する質量 m の質点に速度 v= dx / dt に比例する抵抗力が作用するときの運動方程式

m d2x dt2 =−cx −bv （ c ， b ：正定数） - - - (1)

において，単振動の角振動数 ω0 = c/m と減衰率 γ=b/ 2m を導入して整理すると，定数係数の2階同次線形微分方程式

d2x dt2 +2γ dx dt + ω02x =0 - - - (2)

が得られる．この特性方程式 λ2 + 2γλ + ω02 =0 の解 λ= −γ± γ2 − ω02 は，抵抗が比較的小さくて γ< ω0 ならば共役複素数となり，この場合を不足減衰 (under damping) という． ω= ω02 − γ2 とおくと，式(2)の一般解は

x=A e−γt cos(ωt+α) （ A ， α ：任意定数） - - - (3)

で与えられ，振幅が時間とともに指数関数的に小さくなりながら振動する減衰振動となる（減衰調和振動 : damped harmonic motion）．このとき， ω はこの減衰振動の角振動数を表し，周期は

T= 2πω = 2π ω02 − γ2 - - - (4)

で与えられる．必ず ω< ω0 なので，周期は単振動のときより大きくなる（不足減衰のシミュレーション）．質点の速度は

v= dx dt =−A e−γt { γcos (ωt+α) + ωsin (ωt+α) } - - - (5)

であり，初期条件として， x(0) =x0 ， v(0) =v0 を考えると，任意定数 A と α は

A2 = x02 + ( x0γ + v0 ) 2 ω2 ， tanα=− x0 γ+ v0 x0 ω - - - (6)

を満たすように決定される（ x0 =0 のときは， cosα=0 を満たす α を考えればよい）．

γ=0.1 s -1 ， ω=1.0 s -1 の場合について，初期条件 x(0) =1.0 m ， v(0) =0 m/s の解（青線）と初期条件 x(0) =0 m ， v(0) =1.0 m/s の解（赤線）を下図に示す．

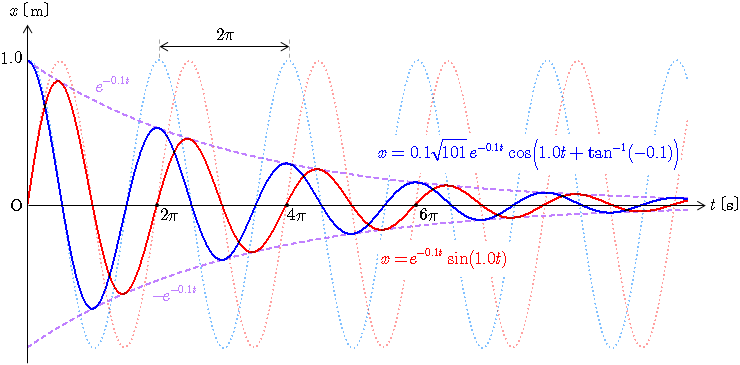
式(5)において，速度 v= dx dt =0 とおくと位置 x が極大または極小になるときの時刻が得られる．その時刻は

γcos (ωt+α) + ωsin (ωt+α) =0 ⇒ tan (ωt+α) =− γω ⇒ ωt+α =nπ+ tan−1 (−γω)

より求められる（ここで， n は1から始まる整数とする）．したがって，図からもわかるように極大・極小となる時刻は複数あり， n 番目に極大または極小となる時刻 tn は次式となる．

tn = 1ω ( nπ− tan−1 γω −α ) ， n= 1 , 2 , 3 , ⋯ - - - (7)

式(7)を式(3)に代入すると，このときの x の絶対値は

| x(tn) | = | Acos( nπ− tan−1 γω ) | exp[ −γω ( nπ− tan−1 γω −α ) ]

となり，

cos( nπ− tan−1 γω ) = cos(nπ) cos( tan−1 γω ) + sin(nπ) sin( tan−1 γω ) ，

cos(nπ) =±1 ， sin(nπ) =0 ， cos( tan−1 γω ) = ω ω2 + γ2 = ω ω02 = ω ω0

であるので，

| x( tn ) | = |A| ω ω0 exp[ − γω nπ + γω tan−1 γω + γω α ] - - - (8)

となる．上式の対数をとると

log| x ( tn ) | = C− γω nπ （ C ：定数） - - - (9)

の形になっている．ここで，定数

C= log|A| + log ω ω0 + γω tan−1 γω + γω α

である．式(9)は，1往復毎( n が2増す毎）に，つまり，周期 T 経過毎に， γT= 2πγ /ω ずつ減少していく．この無次元量 γT を対数減衰度 (logarithmic damping decrement) という．

減衰振動 ： 不足減衰 (under damping)