角速度 (angular velocity)

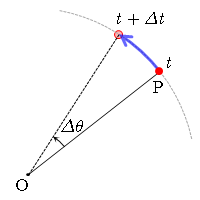
ある点 O のまわりで点 P が回転運動をするとき，その回転運動している平面において動径 OP が単位時間当たりに回転する角度，つまり角度の時間変化率を 角速度 (angular velocity) という．一般に，角速度の符号は，回転平面において点 P が反時計回りに回転する向きを正とし，時計回りの向きを負とするように定義する．

国際単位系（SI）では，角速度の単位として [rad/s] ，あるいは rad を省略して単に [ s−1 ] を用い，1秒間あたりに回転する角度(ラジアン単位)を表す．

時刻 t から t+Δt の間に点 P が角 Δθ だけ回転したとき，この間の角度の平均変化率を平均の角速度といい，

ω¯ = Δθ Δt     - - - (1)

で表す．上式において Δt→0 の極限をとると，（瞬間）角速度

ω= lim Δt→0 Δθ Δt = dθ dt     - - - (2)

が得られる．したがって，逆に角度 θ は角速度 ω を時刻 t について積分

θ= ∫ωdt     - - - (3)

することにより得られる．

便宜上，角速度は大きさ | dθ dt | をもち，点 P の回転する向きに回る右ネジの進む方向を向いたベクトル（角速度ベクトル）として扱われることがある．このとき，角速度ベクトルは回転軸の向きに一致し，角速度ベクトルの先から回転面を見ると点 P は反時計回りに回転している．つまり，角速度ベクトルの向きは回転面が反時計回りに見える方向を向くように定義される．

ホーム>>カテゴリー分類>>力学>>運動>>回転運動>>角速度