回転運動 (rotational motion)
時間
Δt
の間に,点もしくは物体が平面内にある点 O を中心にその平面内において半径
R
で角
Δθ
回転するような運動を 回転運動 (rotational motion) という.その軌跡が1周せずに弧の場合でも回転運動に含まれる.
このとき,点 O を 回転中心 (rotation center),半径
R
を 回転半径 (turning radius),点もしくは物体が回転する平面を 回転面 (surface of revolution) という.また,回転面に垂直で回転中心 O を通る軸を 回転軸 (axis of rotation) という.
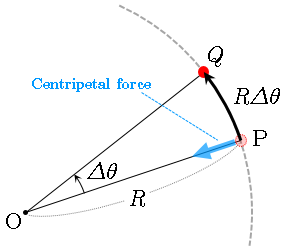
図のように,物体(赤丸)が点 O を回転中心として角
Δθ
だけ回転して点 P から点 Q に移動したとき,かかった時間を
Δt
として,その時間内では回転半径
R
が一定だとする.点 P から点 Q への移動距離は
RΔθ
であり,このとき,物体の平均の速さ
v¯
は
v¯
=
RΔθ
Δt
=R
Δθ
Δt
=R
ω¯
と表される.ここで,
ω¯
=
Δθ
/
Δt
は単位時間あたりに回る平均の角度(平均の角速度)を表す.ここで,
Δt→0
の極限をとると,(瞬間)角速度
ω=
lim
Δt→0
Δθ
Δt
=
dθ
dt
が得られる.一般には,角速度や回転半径は一定ではなく時々刻々変化する場合があり,回転半径が変化する場合は回転中心も時々刻々変化していく.特に,回転半径が常に一定の運動を 円運動 (circular motion)といい,単に回転運動というと円運動のことを指す場合が多い.
回転運動する物体には,必ずその物体の速度方向と平行でない力が物体に作用している.この力を速度方向(軌跡の接線方向)の成分と速度と直交する方向(軌跡の法線方向)の成分に分解したとき,力の法線方向成分は回転中心を向いていることから,この法線方向の力を 向心力 (centripetal force)という.
ホーム>>カテゴリー分類>>力学>>運動>>回転運動