楕円運動 (elliptical motion)
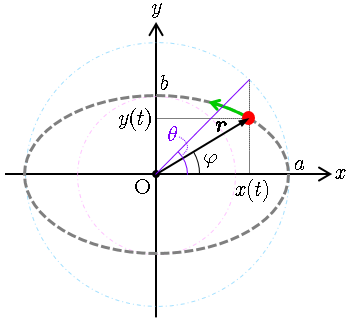
回転運動の軌道が楕円の場合,その運動を 楕円運動 (elliptical motion) という.
点 O を楕円の中心として長半径
と表せる(
の関係がある.
曲線の曲率半径から,角
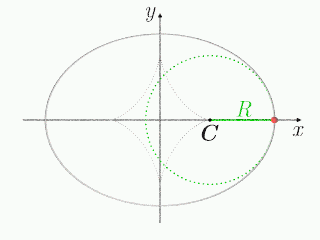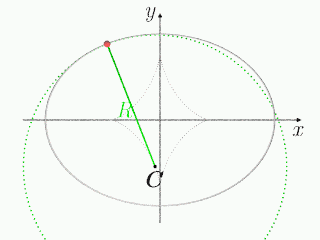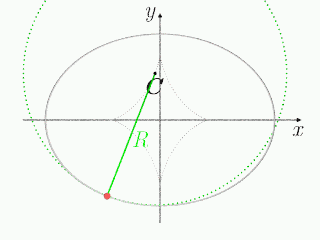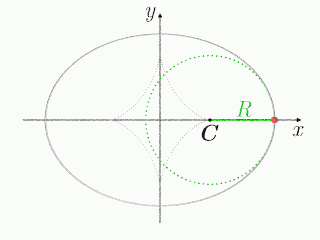
で,回転中心の位置
で与えられ,時々刻々変化する.
2つの惑星の間に中心力の一種である万有引力が作用し互いに束縛して運動する場合,運動する惑星の軌道は一般に楕円軌道となることが知られている.

回転運動の軌道が楕円の場合,その運動を 楕円運動 (elliptical motion) という.
点 O を楕円の中心として長半径
と表せる(
の関係がある.
曲線の曲率半径から,角

で,回転中心の位置
で与えられ,時々刻々変化する.
2つの惑星の間に中心力の一種である万有引力が作用し互いに束縛して運動する場合,運動する惑星の軌道は一般に楕円軌道となることが知られている.