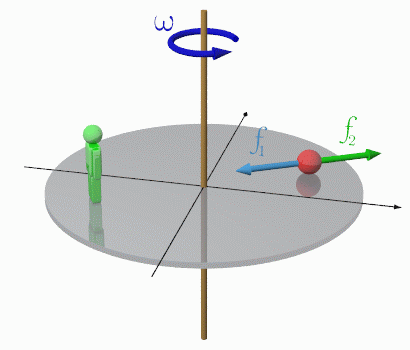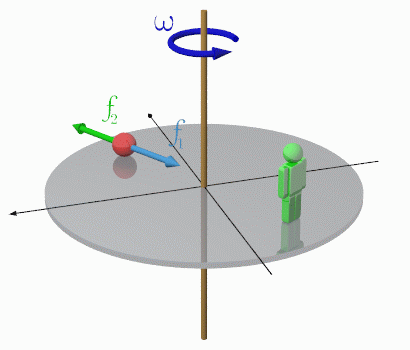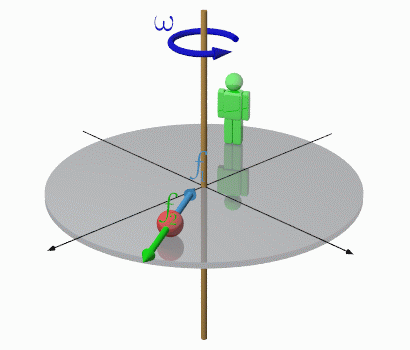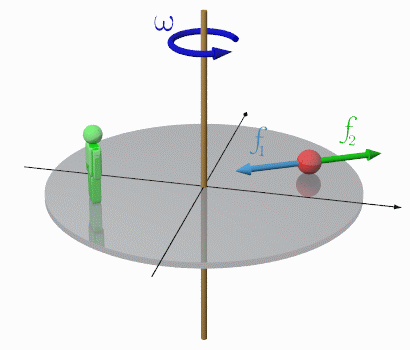
遠心力 (centrifugal force)

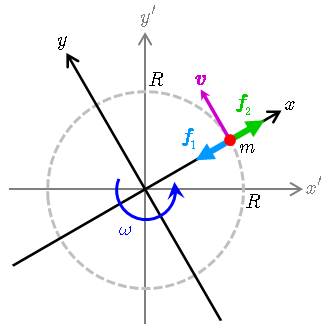
図のように，静止系（慣性系： x′ y′ 座標系）において角速度 ω で半径 R の円運動している質量 m の物体（赤丸）には，物体の速度に垂直で円の中心を向いている大きさ mR ω2 の向心力 (centripetal force) f1 が働いており，その作用により回転運動を実現している．

一方，この物体と共に回転する回転座標系（ xy 座標系）において物体は静止しており，向心力と釣り合う力 f2 が作用しているように見える．この見かけの力 f2 は，向心力 f1 と大きさが等しく方向が逆向きであり（ f2 =− f1 ），物体を回転の中心から遠ざける向きに作用することから 遠心力 (centrifugal force) と呼ばれる．遠心力 f2 は慣性系に対して回転している回転座標系（非慣性系）における慣性力の一つである．

角速度 ω で回転している円盤上に静止している物体を，円盤と一緒に回転している観測者から見ると，物体には向心力 f1 と釣り合う遠心力 f2 が作用しているように感じる．

半径 R の円運動の速さは v=Rω と表せるので，向心力及び遠心力の大きさは

| f1 | = | f2 | = mv2 R

となる．円軌道に限らず，曲線軌道を速さ v で運動している質量 m の物体には，その曲線軌道の曲率半径を R とすると，その物体と共に運動する非慣性系において，大きさ mv2 R の遠心力が作用している．

ホーム>>カテゴリー分類>>力学>>運動>>回転運動>>遠心力