円運動 (circular motion)

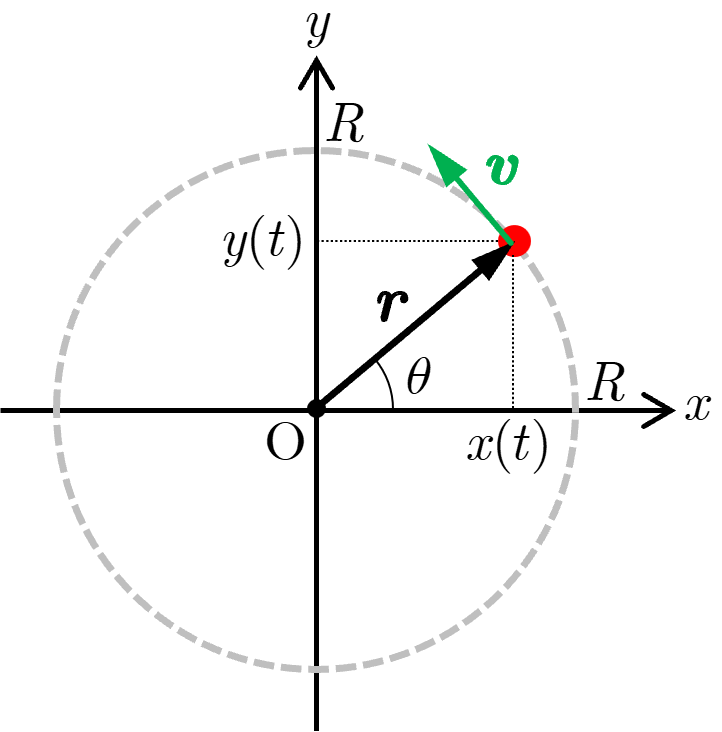
回転運動の間，回転半径が常に一定であれば，その運動を 円運動 (circular motion) という．この場合，回転中心は変化しない．

図のように，点 ${\displaystyle \text{O}}$ を回転中心として，一定の半径 ${\displaystyle R}$ の円運動している質点の位置 ${\displaystyle \mathit{r}}$ は， ${\displaystyle x}$ 軸から測った角度 ${\displaystyle \theta }$ を用いて

${\displaystyle \mathit{r}=(x,y)=(R\cos \theta ,R\sin \theta )}$     ---- (1)

と表せる．ここで， ${\displaystyle \theta }$ は時刻 ${\displaystyle t}$ の関数である（ ${\displaystyle \theta =\theta (t)}$ ）．円運動している質点の速度 ${\displaystyle \mathit{v}}$ は

${\displaystyle \mathit{v}=(v_x,v_y)}$ ${\displaystyle =\frac{d\mathit{r}}{dt}}$ ${\displaystyle =(\frac{dx}{dt},\frac{dy}{dt})}$
   ${\displaystyle =(-R\sin \theta \cdot \frac{d\theta }{dt},R\cos \theta \cdot \frac{d\theta }{dt})}$
   ${\displaystyle =(-R\omega \sin \theta ,R\omega \cos \theta )}$     ---- (2)

となる．ここで， ${\displaystyle \omega =\frac{d\theta }{dt}}$ は角速度を表す．内積 ${\displaystyle \mathit{r}\cdot \mathit{v}=0}$ より，位置 ${\displaystyle \mathit{r}}$ と速度 ${\displaystyle \mathit{v}}$ は直交する．また，質点の速さ ${\displaystyle v}$ は

${\displaystyle v=\left|\mathit{v}\right|=\sqrt{v_x^2+v_y^2}}$ ${\displaystyle =\sqrt{R^2{\omega }^2({\sin }^2\theta +{\cos }^2\theta )}}$ ${\displaystyle =R\left|\omega \right|}$     ---- (3)

となる．特に，円運動の速さが常に一定である運動を等速円運動という．式(3)から速さが一定ということは角速度が一定ということである．

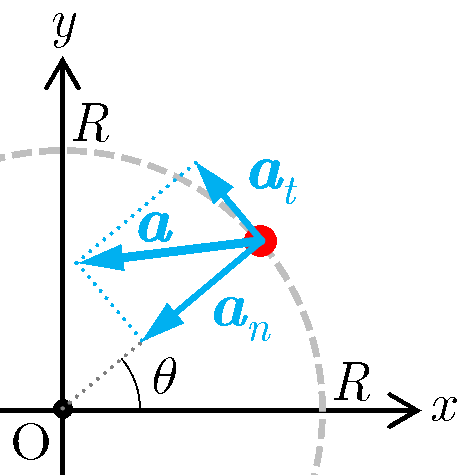
円運動している質点の加速度 ${\displaystyle \mathit{a}}$ は

${\displaystyle \mathit{a}=(a_x,a_y)}$ ${\displaystyle =\frac{d\mathit{v}}{dt}}$ ${\displaystyle =(\frac{d{v}_x}{dt},\frac{d{v}_y}{dt})}$
   ${\displaystyle =(-R\frac{d\omega }{dt}\sin \theta -R\omega \cos \theta \cdot \frac{d\theta }{dt},R\frac{d\omega }{dt}\cos \theta -R\omega \sin \theta \cdot \frac{d\theta }{dt})}$
   ${\displaystyle =(-R\alpha \sin \theta -R{\omega }^2\cos \theta ,R\alpha \cos \theta -R{\omega }^2\sin \theta )}$
   ${\displaystyle =\frac{\alpha }{\omega }(-R\omega \sin \theta ,R\omega \cos \theta )}$ ${\displaystyle -{\omega }^2(R\cos \theta ,R\sin \theta )}$
   ${\displaystyle =\frac{\alpha }{\omega }\mathit{v}-{\omega }^2\mathit{r}}$     ---- (4)

となる．ここで， ${\displaystyle \alpha =\frac{d\omega }{dt}}$ は角加速度を表す．式(4)の第1項目は速度 ${\displaystyle \mathit{v}}$ と平行なので円軌道の接線方向を向いており，第2項目は位置 ${\displaystyle \mathit{r}}$ と逆向きなので円の中心方向（法線方向）を向いている．したがって，

${\displaystyle {\mathit{a}}_t=\frac{\alpha }{\omega }\mathit{v}}$ ,    ${\displaystyle {\mathit{a}}_n=-{\omega }^2\mathit{r}}$

をそれぞれ接線加速度，向心加速度（または法線加速度）という．内積 ${\displaystyle {\mathit{a}}_t\cdot {\mathit{a}}_n=0}$ より，これらは直交している．また，これらの大きさは

${\displaystyle a_t=\left|\frac{\alpha }{\omega }\mathit{v}\right|}$ ${\displaystyle =\left|\frac{\alpha }{\omega }\cdot R\omega \right|}$ ${\displaystyle =R\left|\alpha \right|}$ ,    ${\displaystyle a_n=\left|-{\omega }^2\mathit{r}\right|}$ ${\displaystyle =R{\omega }^2}$

であり，加速度 ${\displaystyle \mathit{a}}$ の大きさは

${\displaystyle a=\sqrt{a_t^2+a_n^2}=R\sqrt{{\alpha }^2+{\omega }^4}}$

となる．角加速度がゼロ (${\displaystyle \alpha =0}$) のとき，角速度は一定となるので等速円運動であり，このとき接線加速度はゼロ (${\displaystyle {\mathit{a}}_t=\mathbf{0}}$) となる．

ホーム>>カテゴリー分類>>力学>>運動>>回転運動>>円運動