デルタ関数の公式2
ディラックのデルタ関数
について,方程式
に関して1つ以上の実数解をもち,連続でなめらかな関数
に対し,以下の式が成り立つ.
ここで,
であり,
は方程式
の
番目の実数解を表す(
).
【導出】
方程式
の
個の実数解
(
)
を含む区間
における積分
について,
を微小量として,以下のように各々の解
の近傍(
)における積分に分割する.
右辺の各々の積分について,
とおく置換積分を用いると,
より
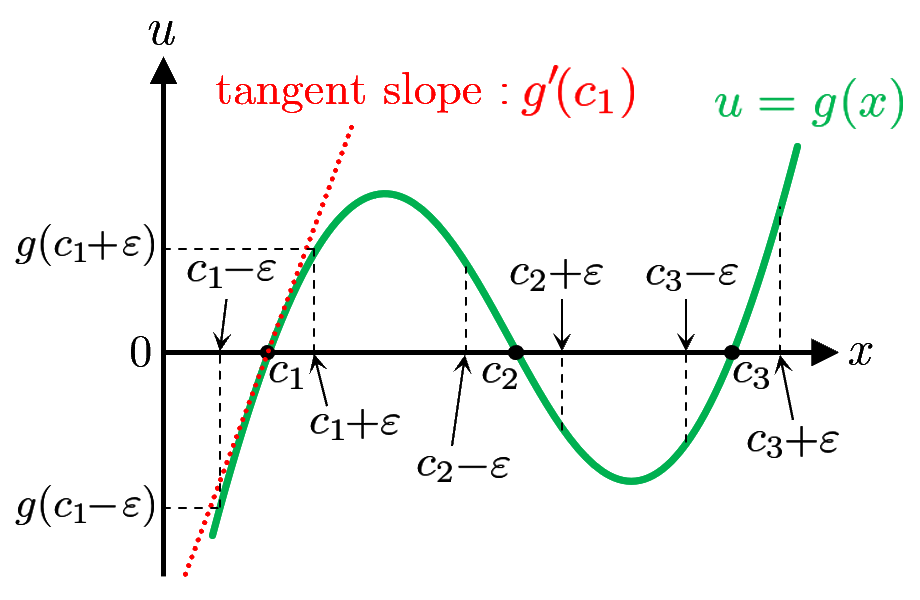
となる.ここで,
での接線の傾き
が正の場合(
),
なので,
が成り立つ.次に,
が負の場合(
),
なので,
が成り立つ.したがって
となり,形式的に
と表せる.
ホーム>>カテゴリー分類>>物理数学>>特殊関数>>デルタ関数の公式2