デルタ関数 (delta function)
のときに値が で, を含む区間で積分すると となる特殊関数 を(ディラックの)デルタ関数 (delta function) といい,
for
で定義される( は より大きい任意の数).
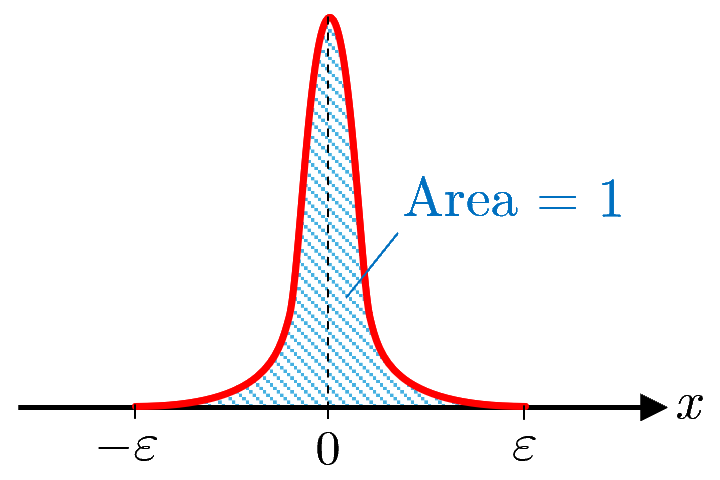
図1 デルタ関数のイメージ
で
なので は偶関数であり,
である.また,積分すると有限の値をとることから
となる.
このデルタ関数は,質量が1点に集中した質点や電荷が1点に集中した点電荷,瞬間に発生するパルス信号などを表すのに便利であり,物理学や工学の分野でよく用いられる(制御工学ではデルタ関数のことをインパルス関数 (impulse function) という).式(1),(2)で定義されるデルタ関数は通常の関数とは異なりグラフで表すことはできないが,図1に示すグラフのようなイメージをもつと良い( はいくらでも小さくとれる).また,デルタ関数を初等関数で近似すると実際にグラフが描ける.
ディラックのデルタ関数 は連続変数に対する関数であり,離散変数に対してはクロネッカーのデルタと呼ばれる関数が存在する.
【デルタ関数の性質】
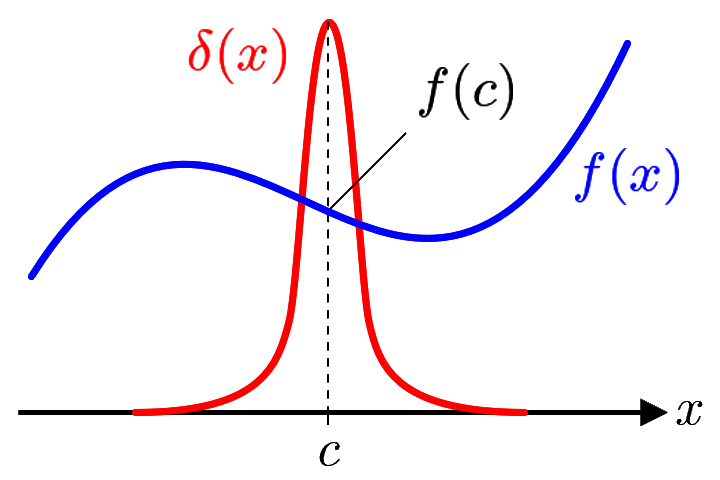
図2 の取り出し
(定数)で連続でなめらかな任意の関数 とデルタ関数 を掛け合わして, を含む区間 で積分すると
となることから,デルタ関数は の での値 を取り出す役割を果たす.この性質が非常に重要であり,元々,この性質を満たす関数としてデルタ関数は定義された.つまり,関数 から での値を取り出す演算を積分で表すためのものであり,デルタ関数を含む式は積分して初めて意味をもつ.通常,積分区間 は から の範囲を考えることが多い.
式(3)において, (定数関数), とすると,デルタ関数の定義式(2)となる.
また,以下の式が成り立つ(ただし,両辺に を掛けて積分した式において成り立つことに注意).
上の式(5)は式(4)の拡張として得られ, であり, は方程式 の 番目の実数解を表す( ).
デルタ関数は,便宜上,様々な初等関数によって近似して用いることがある(デルタ関数の近似).
【3次元空間でのデルタ関数】
1変数関数の は,変数が のみであるので,1次元( 軸上)のデルタ関数である.3次元空間でのデルタ関数 は, として
で定義される.3次元の場合,式(3)は
と表される.ここで, である.