デルタ関数の近似
デルタ関数 は
を満たす様々な初等関数 によって近似的に表すことができる( ).このとき,積分領域 は通常, の範囲で考える.
分数関数による表現
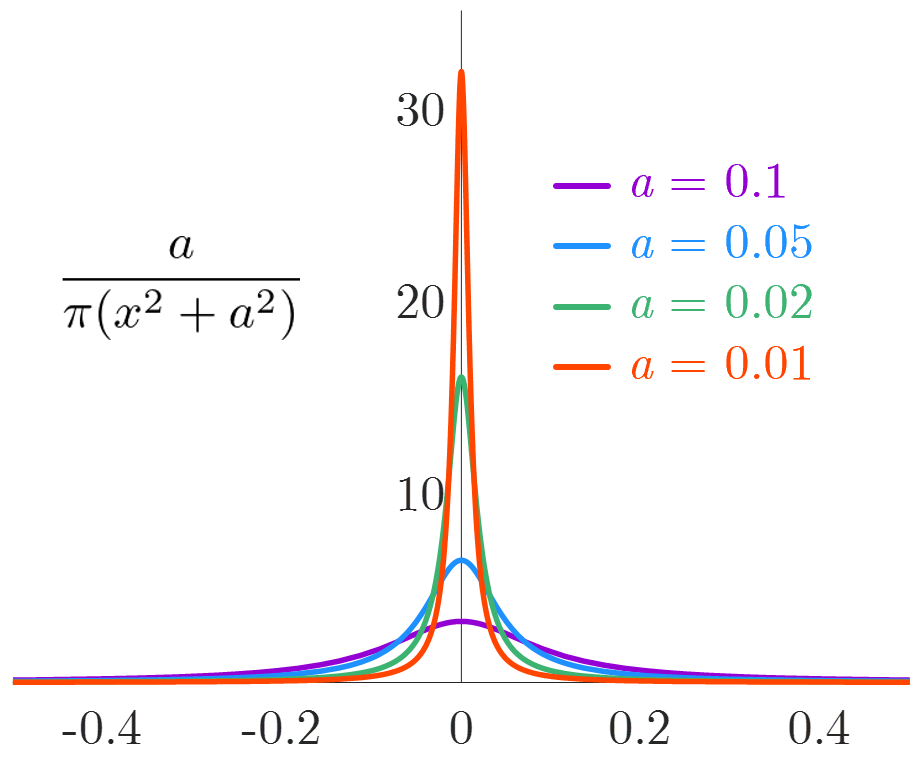
として,以下のように分数関数の極限によってデルタ関数を表現することができる.
この分数関数は の値が小さいほど, に鋭いピークをもつ.式(2)を から まで積分すると, の値にかかわらず
となり,デルタ関数の定義を満たすことが分かる.
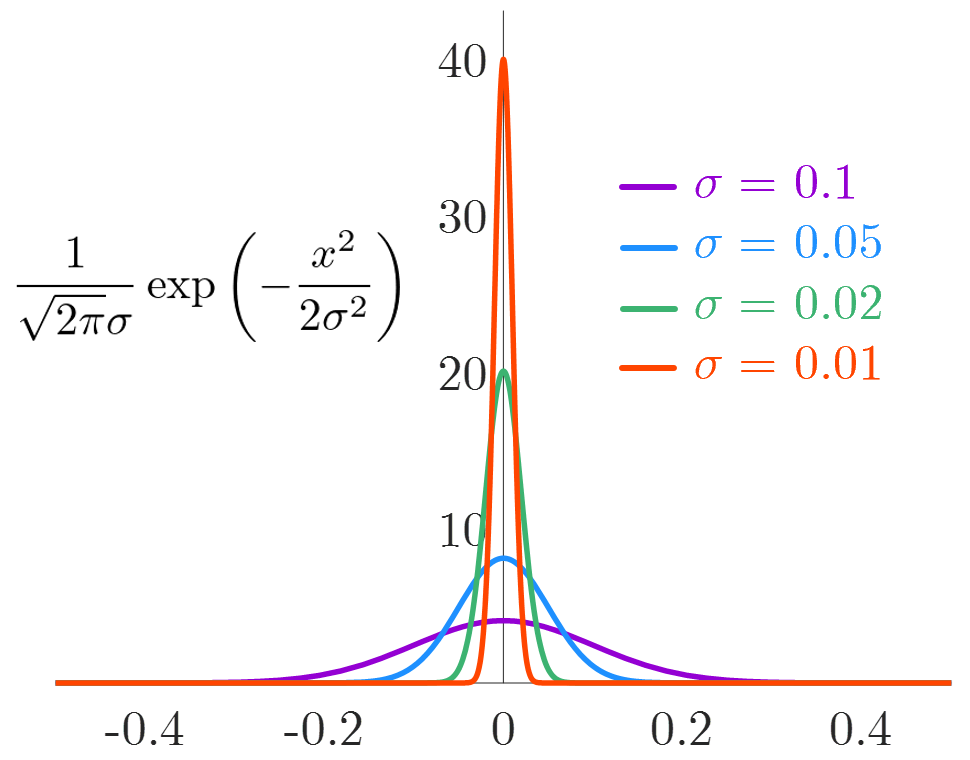
正規分布(ガウス分布)の確率密度関数による表現
三角関数を用いた表現
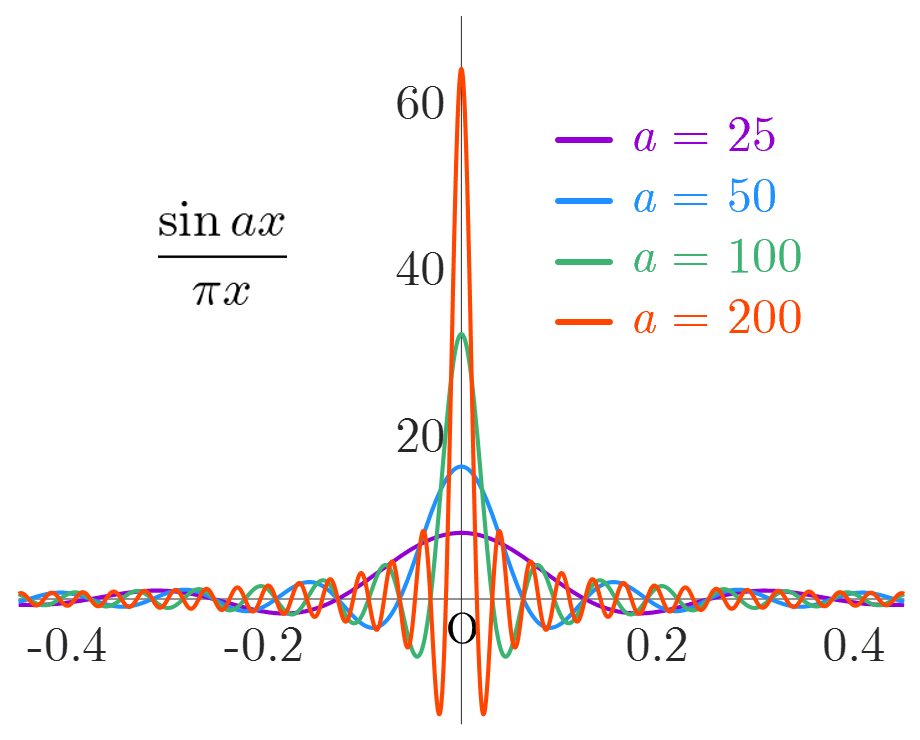
sinc(シンク)関数 を用いて,次式のようにデルタ関数を表現することができる.
上式2行目の関数は で定義できないが, は の極限で に収束する( と定義される ).関数 は の値が大きいほど, に鋭いピークをもち, から までの積分は の値にかかわらず となる(参考:sinc関数の積分).
物理の分野におけるデルタ関数の表現として,式(4)はよく出てくる.
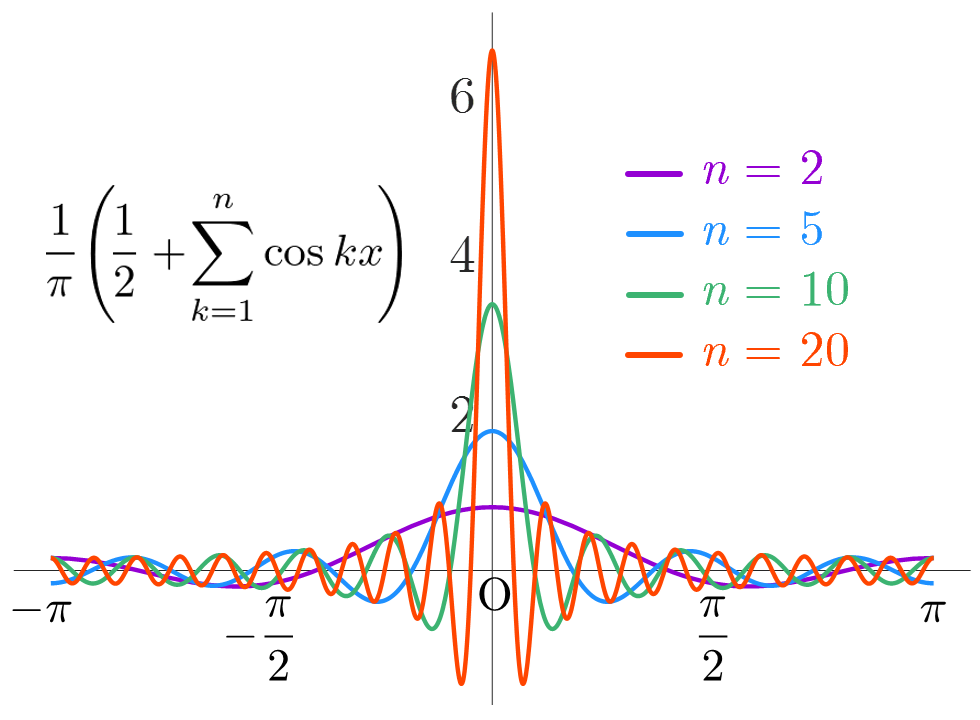
また, 関数を用いて
のように定義された関数 について,定義域を から に制限して の極限をとると,デルタ関数を表現することができる.
は が大きいほど, に鋭いピークをもつ.定義域を から に制限するのは, が周期 の周期関数であるからであり, の値にかかわらず 周期にわたる積分が となる.
のとき, を以下のように変形できる.
ここで,積和の公式 を用いた.上式の 内の和を書き下すと,以下のように隣り合う項が打ち消し合い
が得られる.したがって,式(5)は
と表せる. のときは,元々の定義式(5)より である.式(7)において, 近傍での振る舞いを考えると と近似できるので,
と表せる.この表式において, を (正の実数)と置き換え, 近傍だけでなく全領域に広げると, の極限で式(4)のデルタ関数の表現に一致する(グラフの形が似ていることにも納得であろう).