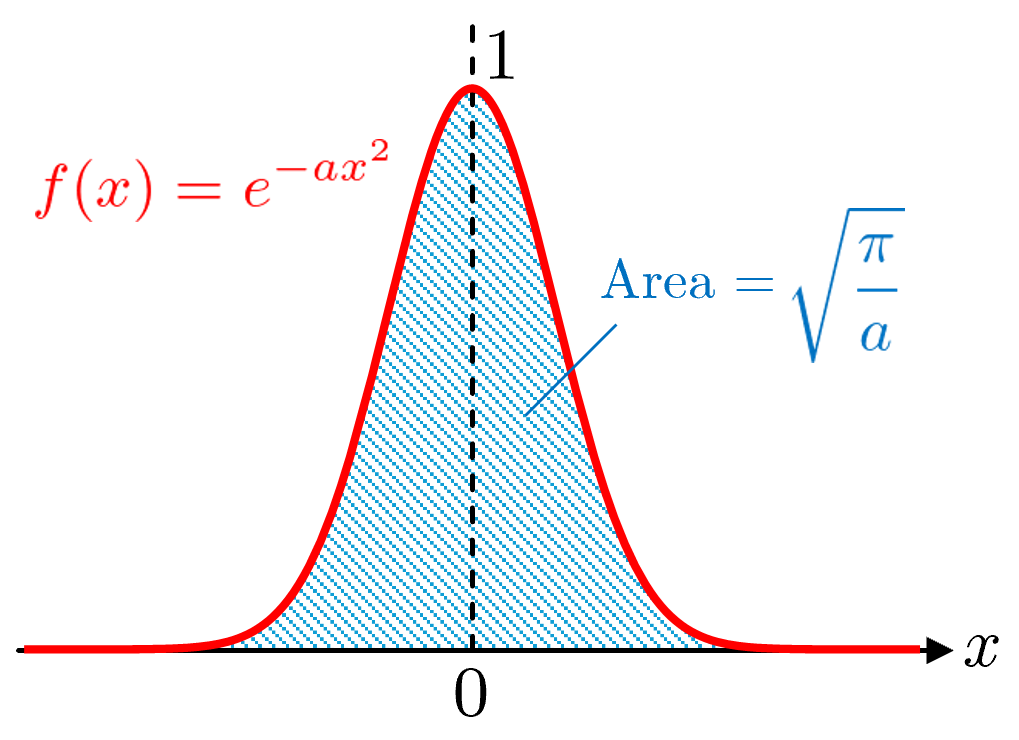
ガウス積分 (Gaussian integral)
とする関数
の
から
までの積分
をガウス積分 (Gaussian integral) という.
ガウス分布(正規分布)の確率密度関数の積分の計算などで出てくる.
【証明】
重積分と極座標を利用して証明する.まず,
より
と書ける.次に,平面の極座標
を用いて,変数変換
,
を行うと
であり,
重積分における変数変換よりヤコビアンは
なので,
と置き換わる.したがって,
が得られ,
が求まる.
ホーム>>カテゴリー分類>>物理数学>>解析学>>ガウス積分